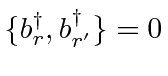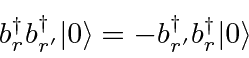At this point, we can hypothesize that the operators that create fermion states do not commute.
In fact, if we assume that the operators creating fermion states anti-commute (as do the Pauli matrices),
then we can show that fermion states are antisymmetric under interchange.
Assume
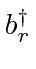 and
and
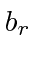 are the creation and annihilation operators for fermions and that they anti-commute.
The states are then antisymmetric under interchange of pairs of fermions.
are the creation and annihilation operators for fermions and that they anti-commute.
The states are then antisymmetric under interchange of pairs of fermions.
Its not hard to show that the occupation number for fermion states is either zero or one.
Jim Branson
2013-04-22