Next: Fermion Operators Up: Quantum Theory of Radiation Previous: Quantization of the Oscillators Contents
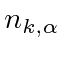 is the number of photons in the volume with wave number
is the number of photons in the volume with wave number
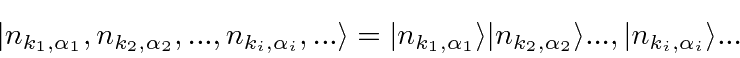
The ground state for a particular oscillator cannot be lowered.
The state in which all the oscillators are in the ground state is called the vacuum stateand can be written simply as
![]() .
We can generate any state we want by applying raising operators to the vacuum state.
.
We can generate any state we want by applying raising operators to the vacuum state.
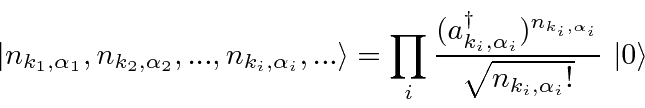
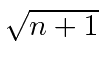 we get from the raising operators.
we get from the raising operators.
Any multi-photon state we construct is automatically symmetric under the interchange of pairs of photons.
For example if we want to raise two photons out of the vacuum, we apply two raising operators.
Since
![\bgroup\color{black}$[a_{k,\alpha}^\dagger,a_{k',\alpha'}^\dagger]=0$\egroup](img3947.png) , interchanging the photons gives the same state.
, interchanging the photons gives the same state.
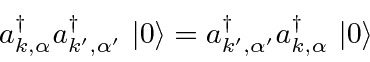
Jim Branson 2013-04-22