Next: Photon States Up: Quantum Theory of Radiation Previous: Canonical Coordinates and Momenta Contents
To summarize the result of the calculations of the last section we have the Hamiltonian for the radiation field.
![\bgroup\color{black}$\displaystyle H=\sum\limits_{k,\alpha}\left({\omega\over c}...
...ht)^2\left[c_{k,\alpha}c_{k,\alpha}^*+c_{k,\alpha}^*c_{k,\alpha}\right] $\egroup](img3924.png)
|
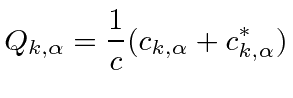
|
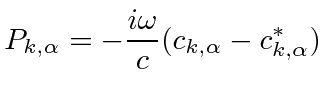
|
![\bgroup\color{black}$\displaystyle H={1\over 2}\sum\limits_{k,\alpha}\left[P_{k,\alpha}^2+\omega^2Q_{k,\alpha}^2\right] $\egroup](img3927.png) |
![\bgroup\color{black}$[p_x,x]={\hbar\over i}$\egroup](img3928.png) .
Coordinates and momenta that do not correspond, do commute.
For example
.
Coordinates and momenta that do not correspond, do commute.
For example
![\bgroup\color{black}$[p_y,x]=0$\egroup](img3929.png) .
Different coordinates commute with each other as do different momenta.
We will impose the same rules here.
.
Different coordinates commute with each other as do different momenta.
We will impose the same rules here.
![\begin{eqnarray*}
\left[Q_{k,\alpha},P_{k',\alpha'}\right]&=&i\hbar\delta_{kk'}\...
...\right]&=&0 \\
\left[P_{k,\alpha},P_{k',\alpha'}\right]&=&0 \\
\end{eqnarray*}](img444.png)
Since we are dealing with harmonic oscillators, we want to find the analog of the raising and lowering operators.
We developed the raising and lowering operators by trying to write the Hamiltonian as
![]() .
Following the same idea, we get
.
Following the same idea, we get
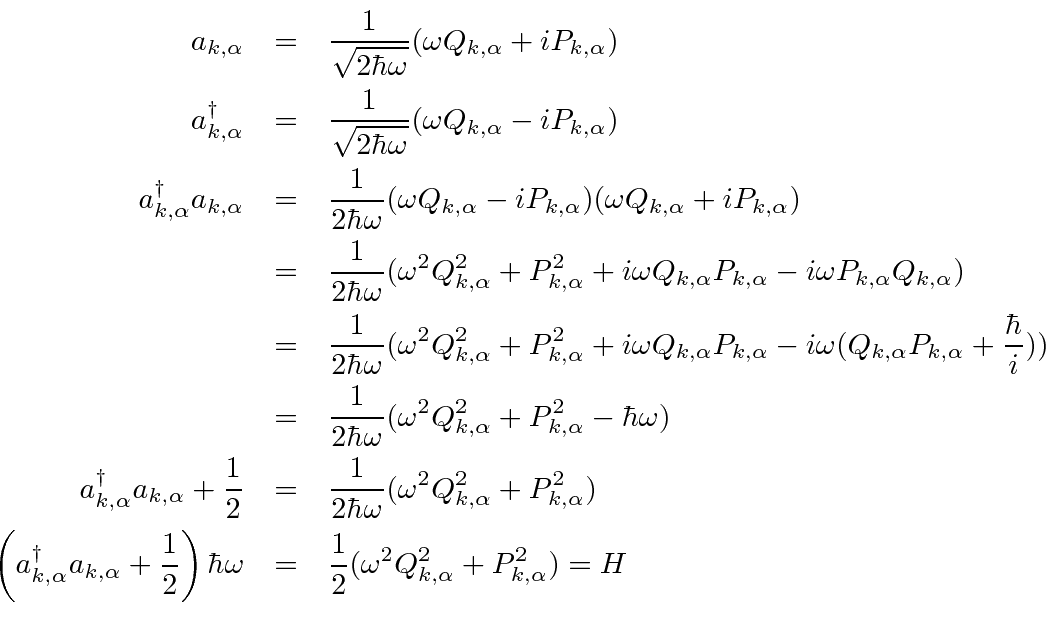
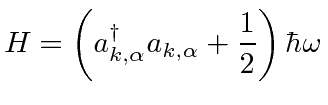 |
![\bgroup\color{black}$[a_{k,\alpha},a_{k,\alpha}^\dagger]=1$\egroup](img3936.png) ,
as we had for the 1D harmonic oscillator.
,
as we had for the 1D harmonic oscillator.
![\begin{eqnarray*}
\left[a_{k,\alpha},a_{k,\alpha}^\dagger\right]&=&[{1\over\sqrt...
...r 2\hbar\omega}\left(\hbar\omega+\hbar\omega\right) \\
&=&1 \\
\end{eqnarray*}](img3937.png)
![\begin{displaymath}\bgroup\color{black} [a_{k,\alpha},a_{k',\alpha'}^\dagger]=\delta_{kk'}\delta_{\alpha\alpha'} \egroup\end{displaymath}](img3938.png)
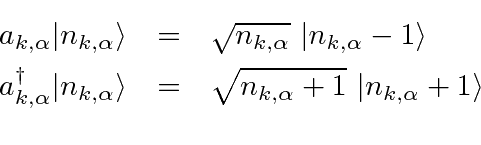
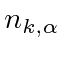 can only take on integer values as with the harmonic oscillator we know.
can only take on integer values as with the harmonic oscillator we know.
As with the 1D harmonic oscillator, we also can define the number operator.
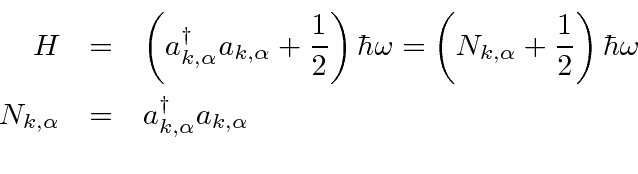
The last step is to compute the raising and lowering operators in terms of the original coefficients.
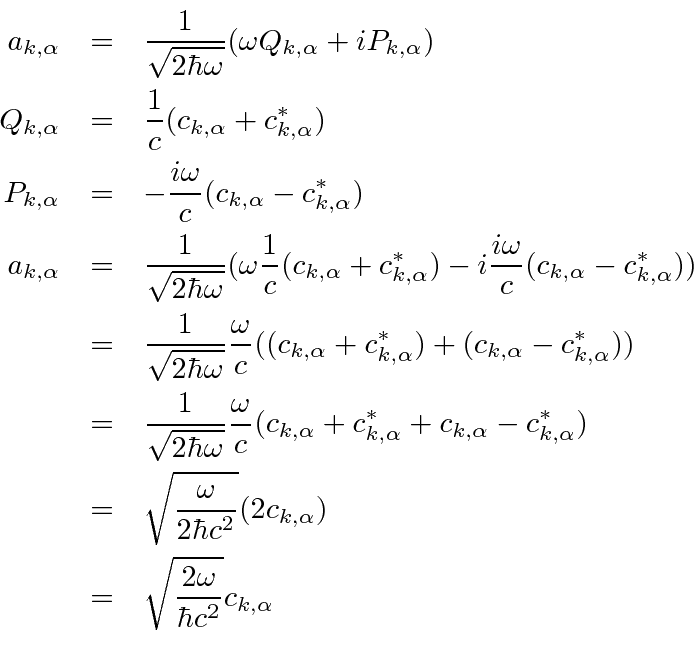
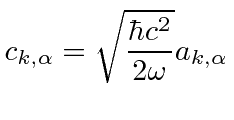 |
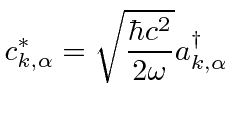 |
Jim Branson 2013-04-22