Canonical Coordinates and Momenta

We now have the Hamiltonian for the radiation field.

$$H=\sum\limits_{k,\alpha}\left({\omega\over c}... ..._{k,\alpha}(t)c_{k,\alpha}^*(t)+c_{k,\alpha}^*(t)c_{k,\alpha}(t)\right]$$

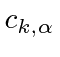It was with the Hamiltonian that we first quantized the non-relativistic motion of particles. The position and momentum became operators which did not commute. Lets define $c_{k,\alpha}$ to be the time dependent Fourier coefficient.

$$\bgroup\color{black} \ddot{c}_{k,\alpha}=-\omega^2c_{k,\alpha} \egroup$$

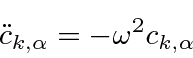
We can then simplify our notation a bit.

$$\bgroup\color{black} H=\sum\limits_{k,\alpha}\left({\omega\ov... ...\alpha}c_{k,\alpha}^*+c_{k,\alpha}^*c_{k,\alpha}\right] \egroup$$

This now clearly looks like the Hamiltonian for a collection of uncoupled oscillators; one oscillator for each wave vector and polarization.

We wish to write the Hamiltonian in terms of a coordinate for each oscillator and the conjugate momenta. The coordinate should be real so it can be represented by a Hermitian operator and have a physical meaning. The simplest choice for a real coordinates is 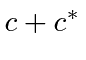$c+c^*$. With a little effort we can identify the coordinate

$$\bgroup\color{black} Q_{k,\alpha}={1\over c}(c_{k,\alpha}+c_{k,\alpha}^*) \egroup$$

and its conjugate momentum for each oscillator,

$$\bgroup\color{black} P_{k,\alpha}=-{i\omega\over c}(c_{k,\alpha}-c_{k,\alpha}^*). \egroup$$

The Hamiltonian can be written in terms of these.

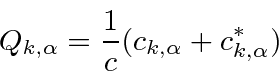
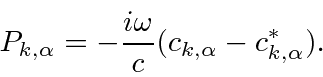
$$\begin{eqnarray*} H&=&{1\over 2}\sum\limits_{k,\alpha}\left[P_{k,\alpha}^2+\omeg... ...c_{k,\alpha}c_{k,\alpha}^*+c_{k,\alpha}^*c_{k,\alpha}\right] \\ \end{eqnarray*}$$

This verifies that this choice gives the right Hamiltonian. We should also check that this choice of coordinates and momenta satisfy Hamilton's equations to identify them as the canonical coordinates. The first equation is

$$\begin{eqnarray*} {\partial H\over\partial Q_{k,\alpha}}&=&-\dot{P}_{k,\alpha} \... ...,\alpha}^*)&=&{\omega^2\over c}(c_{k,\alpha}+c_{k,\alpha}^*) \\ \end{eqnarray*}$$

This one checks out OK.

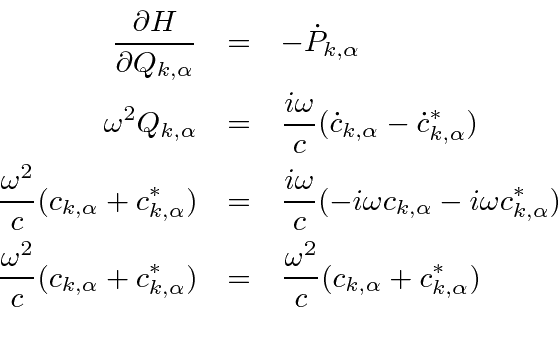
The other equation of Hamilton is

$$\begin{eqnarray*} {\partial H\over\partial P_{k,\alpha}}&=&\dot{Q}_{k,\alpha} \\... ...,\alpha}^*)&=&-{i\omega\over c}(c_{k,\alpha}-c_{k,\alpha}^*) \\ \end{eqnarray*}$$

This also checks out, so we have identified the canonical coordinates and momenta of our oscillators.

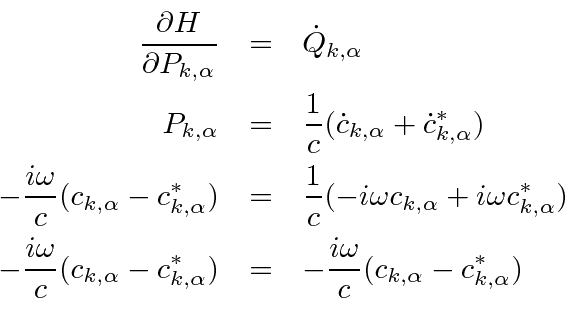
We have a collection of uncoupled oscillators with identified canonical coordinate and momentum. The next step is to quantize the oscillators.