Next: Canonical Coordinates and Momenta Up: Quantum Theory of Radiation Previous: Fourier Decomposition of Radiation Contents
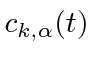 .
This is an important calculation because we will
use the Hamiltonian formalism to do the quantization of the field.
We will do the calculation using the covariant notation (while Sakurai outlines an alternate calculation using 3-vectors).
We have already calculated the Hamiltonian density for a classical EM field.
.
This is an important calculation because we will
use the Hamiltonian formalism to do the quantization of the field.
We will do the calculation using the covariant notation (while Sakurai outlines an alternate calculation using 3-vectors).
We have already calculated the Hamiltonian density for a classical EM field.
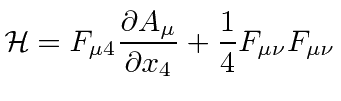 |
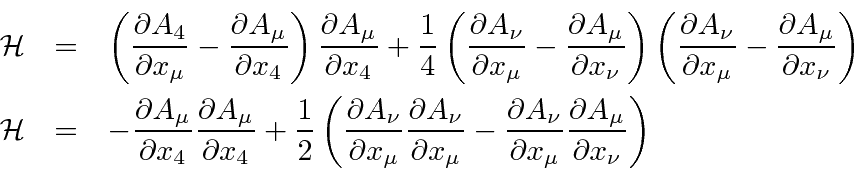
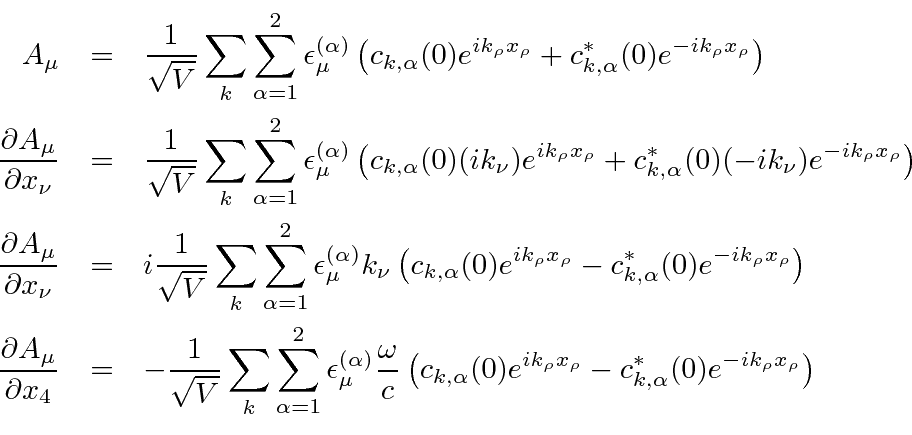
We have all the elements to finish the calculation of the Hamiltonian.
Before pulling this all together in a brute force way,
its good to realize that almost all the terms will give zero.
We see that the derivative of
![]() is proportional to a 4-vector, say
is proportional to a 4-vector, say
![]() and to a polarization vector,
say
and to a polarization vector,
say
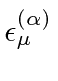 .
The dot products of the 4-vectors, either
.
The dot products of the 4-vectors, either
![]() with itself or
with itself or
![]() with
with
![]() are zero.
Going back to our expression for the Hamiltonian density, we can eliminate some terms.
are zero.
Going back to our expression for the Hamiltonian density, we can eliminate some terms.
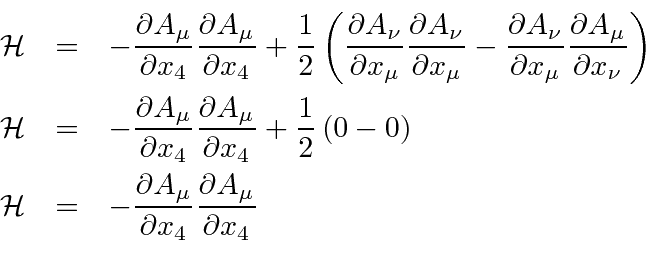
The total Hamiltonian we are aiming at, is the integral of the Hamiltonian density.
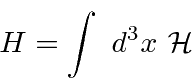
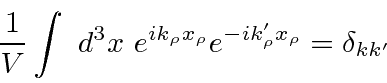
![\begin{eqnarray*}
H&=&\int d^3x {\cal H} \\
{\cal H}&=&-{\partial A_\mu\over\p...
...(t)c_{k,\alpha}^*(t)+c_{k,\alpha}^*(t)c_{k,\alpha}(t)\right] \\
\end{eqnarray*}](img3912.png)
It should not be a surprise that the terms that made up the Lagrangian gave a zero contribution because
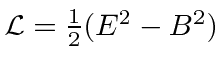 and we know that E and B have the same magnitude in a radiation field.
(There is one wrinkle we have glossed over; terms with
and we know that E and B have the same magnitude in a radiation field.
(There is one wrinkle we have glossed over; terms with
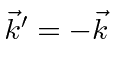 .)
.)
Jim Branson 2013-04-22