Next: Sinusoidal Perturbations Up: Time Dependent Perturbation Theory Previous: Time Dependent Perturbation Theory Contents
Assume that we solve the unperturbed energy eigenvalue problem exactly:
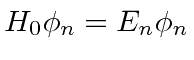 .
Now we add a perturbation that depends on time,
.
Now we add a perturbation that depends on time,
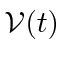 .
Our problem is now inherently time dependent so we go back to the
time dependent Schrödinger equation.
.
Our problem is now inherently time dependent so we go back to the
time dependent Schrödinger equation.
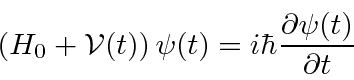
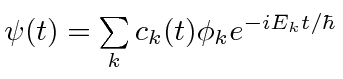 with
with
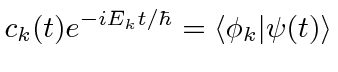 .
The time dependent Schrödinger equations is
.
The time dependent Schrödinger equations is
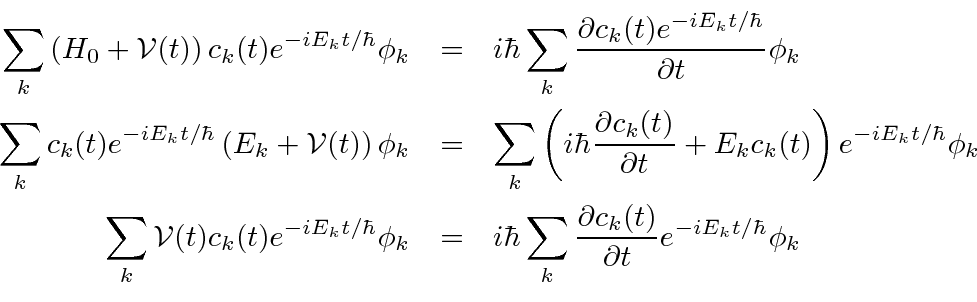
Now dot
 into this equation to get the time dependence of one coefficient.
into this equation to get the time dependence of one coefficient.
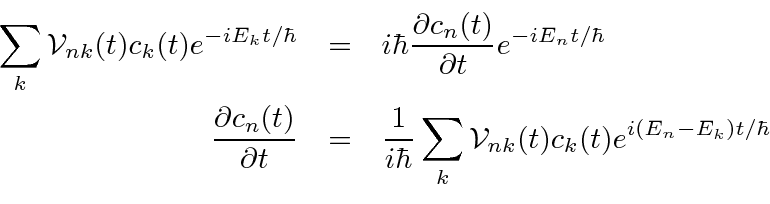
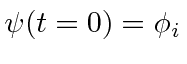 and hence all the other
and hence all the other
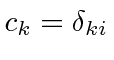 .
.
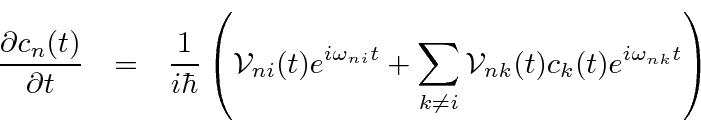
Now we want to calculate transition rates.
To first order, all the
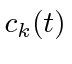 are small compared to
are small compared to
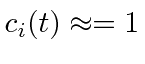 , so the sum can be neglected.
, so the sum can be neglected.
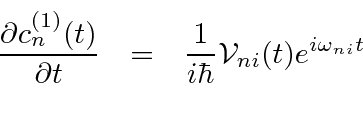
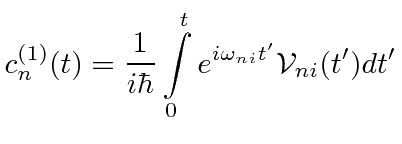 |
Note that, if there is a large energy difference between the initial and final states,
a slowly varying perturbation can average to zero.
We will find that the perturbation will need frequency components compatible with
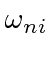 to cause transitions.
to cause transitions.
If the first order term is zero or higher accuracy is required, the second order term can be computed.
In second order, a transition can be made to an intermediate state
![]() , then a transition to
, then a transition to
![]() .
We just put the first order
.
We just put the first order
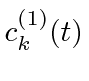 into the sum.
into the sum.
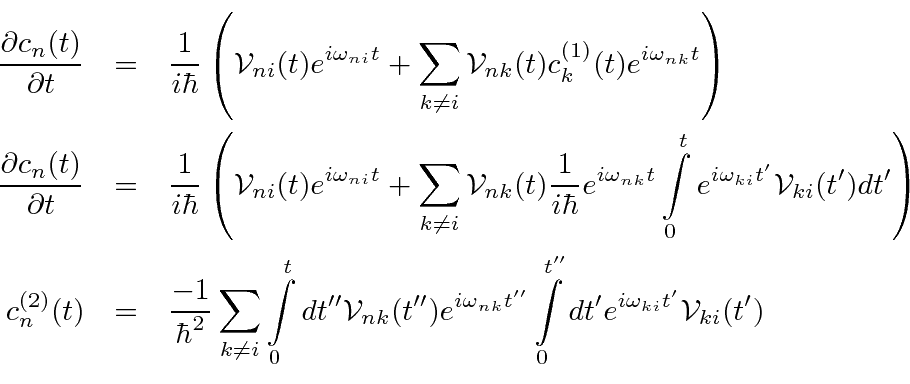
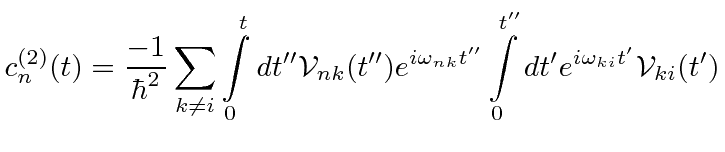 |
* Example:
Transitions of a 1D harmonic oscillator in a transient E field.*
Jim Branson 2013-04-22