Harmonic Oscillator in a Transient E Field
Assume we have an electron in a standard one dimensional harmonic oscillator of frequency
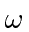 in its ground state.
An weak electric field is applied for a time interval
in its ground state.
An weak electric field is applied for a time interval
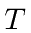 .
Calculate the probability to make a transition to the first (and second) excited state.
.
Calculate the probability to make a transition to the first (and second) excited state.
The perturbation is
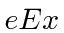 for
for
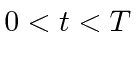 and zero for other times.
We can write this in terms of the raising an lowering operators.
and zero for other times.
We can write this in terms of the raising an lowering operators.
We now use our time dependent perturbation result to compute the transition probability to the first excited state.
As long as the E field is weak, the initial state will not be significantly depleted and the assumption
we have made concerning that is valid.
We do see that the transition probability oscillates with the time during which the E field is applied.
We would get a (much) larger transition probability if we applied an oscillating E field tuned to have
the right frequency to drive the transition.
Clearly the probability to make a transition to the second excited state is zero in first order.
If we really want to compute this, we can use our first order result for
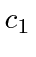 and calculate the
transition probability to the
and calculate the
transition probability to the
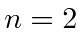 state from that.
This is a second order calculation.
Its not too bad to do since there is only one intermediate state.
state from that.
This is a second order calculation.
Its not too bad to do since there is only one intermediate state.
Jim Branson
2013-04-22
![]() for
for
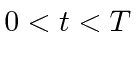 and zero for other times.
We can write this in terms of the raising an lowering operators.
and zero for other times.
We can write this in terms of the raising an lowering operators.
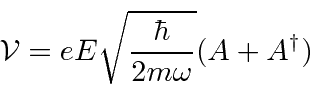
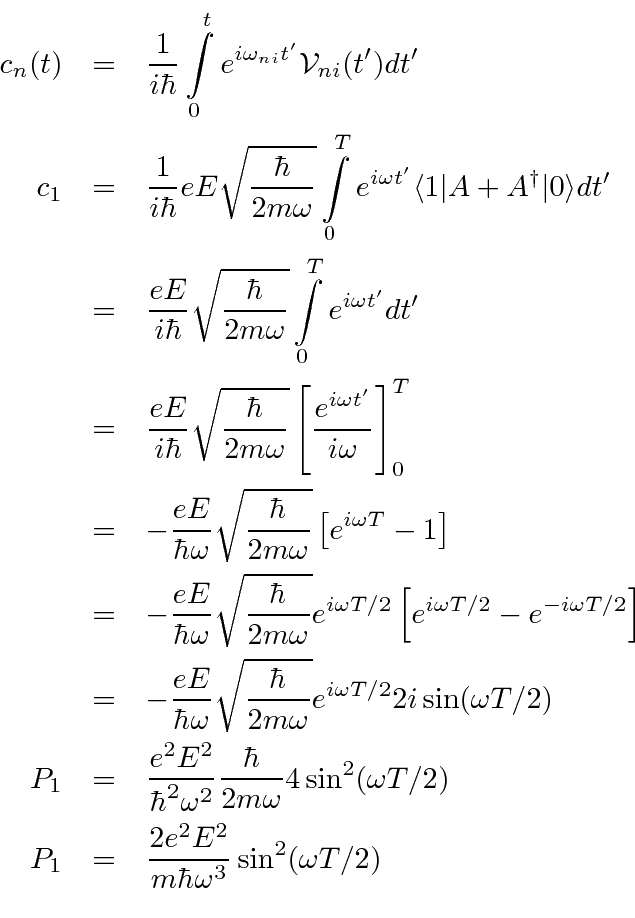
![]() and calculate the
transition probability to the
and calculate the
transition probability to the
![]() state from that.
This is a second order calculation.
Its not too bad to do since there is only one intermediate state.
state from that.
This is a second order calculation.
Its not too bad to do since there is only one intermediate state.