Next: Black Body Radiation Spectrum Up: Review of Radiation of Previous: Review of Radiation of Contents
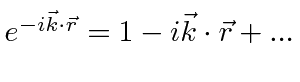 will allow
other transitions to take place but at lower rates.
We will attempt to understand the selection rules when we include the
will allow
other transitions to take place but at lower rates.
We will attempt to understand the selection rules when we include the
The matrix element is proportional to
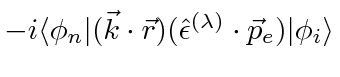 which we will split up into two terms.
You might ask why split it.
The reason is that we will essentially be computing matrix elements of at tensor and dotting it into two vectors
that do not depend on the atomic state.
which we will split up into two terms.
You might ask why split it.
The reason is that we will essentially be computing matrix elements of at tensor and dotting it into two vectors
that do not depend on the atomic state.
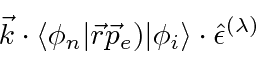
![\begin{eqnarray*}
(\vec{k}\cdot\vec{r})(\hat{\epsilon}^{(\lambda)}\cdot\vec{p}_e...
...)-(\vec{k}\cdot\vec{p})(\hat{\epsilon}^{(\lambda)}\cdot\vec{r})]
\end{eqnarray*}](img4001.png)
The first term can be rewritten.
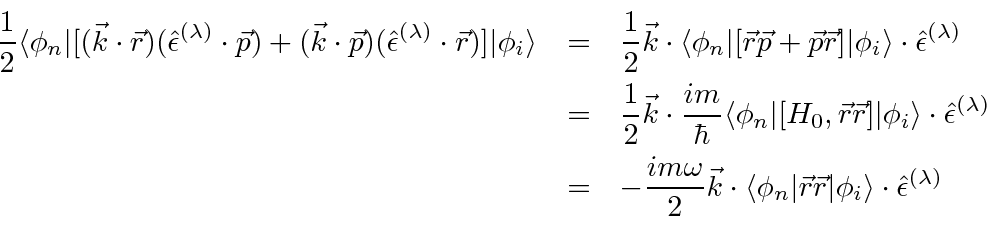
 .
The term proportional to
.
The term proportional to
 .
.
Similarly, the second (anti-symmetric) term can be rewritten slightly.
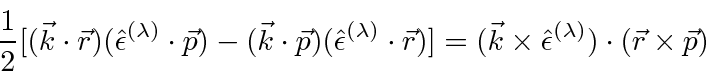
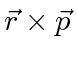 , is an axial vector and therefore has three components.
(Remember and axial vector is the same thing as an anti-symmetric tensor.)
So this is clearly an
, is an axial vector and therefore has three components.
(Remember and axial vector is the same thing as an anti-symmetric tensor.)
So this is clearly an
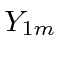 .
Note that it is actually a constant times the orbital angular momentum operator
.
Note that it is actually a constant times the orbital angular momentum operator
So the first term is reasonably named the Electric Quadrupole term because it depends on the quadrupole moment of the state.
It does not change parity and gives us the selection rule.
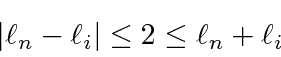
The second term dots the radiation magnetic field into the angular momentum of the atomic state,
so it is reasonably called the magnetic dipole interaction.
The interaction of the electron spin with the magnetic field is of the same order and should be included
together with the E2 and M1 terms.
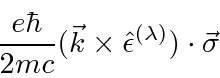
Higher order terms can be computed but its not recommended.
Some atomic states, such as the 2s state of Hydrogen, cannot decay by any of these terms basically because the 2s to 1s is a 0 to 0 transition and there is no way to conserve angular momentum and parity. This state can only decay by the emission of two photons.
While E1 transitions in hydrogen have lifetimes as small as
![]() seconds,
the E2 and M1 transitions have lifetimes of the order of
seconds,
the E2 and M1 transitions have lifetimes of the order of ![]() seconds,
and the 2s state has a lifetime of about
seconds,
and the 2s state has a lifetime of about ![]() of a second.
of a second.
Jim Branson 2013-04-22