Next: Scattering of Photons Up: Quantum Theory of Radiation Previous: Beyond the Electric Dipole Contents
Let's take two atomic states that can make transitions to each other:
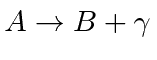 and
and
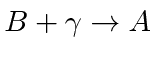 .
From statistical mechanics, we have
.
From statistical mechanics, we have
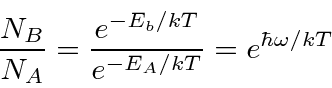
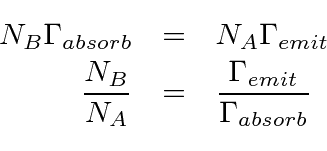
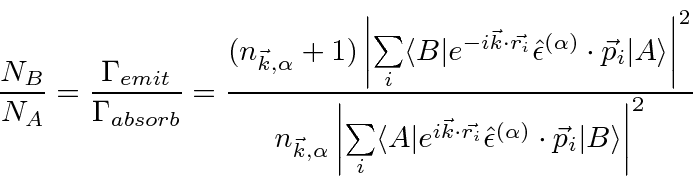
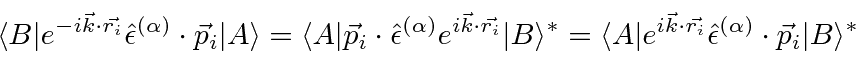
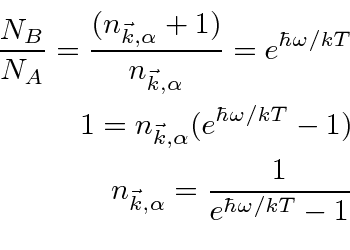
Now suppose the walls of the cavity are black so that they emit and absorb photons at any energy.
Then the result for the number of photons above is true for all the radiation modes of the cavity.
The energy in the frequency interval
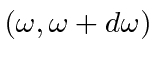 per unit volume can be calculated by
multiplying the number of photons by the energy per photon times the number of modes in that frequency interval
and dividing by the volume of the cavity.
per unit volume can be calculated by
multiplying the number of photons by the energy per photon times the number of modes in that frequency interval
and dividing by the volume of the cavity.
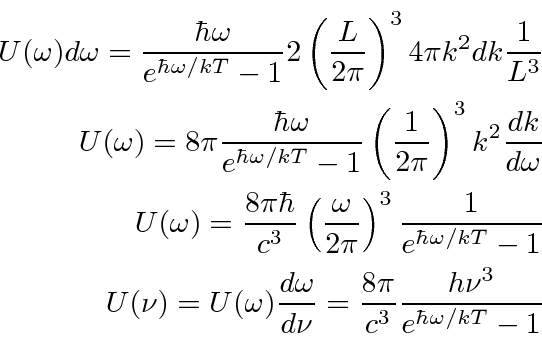
Jim Branson 2013-04-22