Next: The Dirac Equation Up: Course Summary Previous: Scattering of Photons Contents
The quantum self energy correction has important, measurable effects. It causes observable energy shifts in Hydrogen and it helps us solve the problem of infinities due to energy denominators from intermediate states.
The coupled differential equations from first order perturbation theory for the state under study
![]() and
intermediate states
and
intermediate states
![]() may be solved for the self energy correction.
may be solved for the self energy correction.
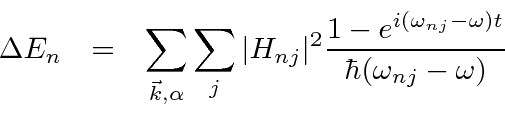
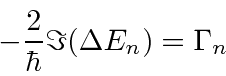
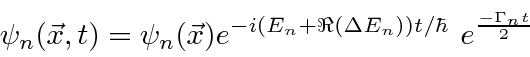
The real part of the correction should be studied to understand relative energy shifts of states. It is the difference between the bound electron's self energy and that for a free electron in which we are interested. The self energy correction for a free particle can be computed.
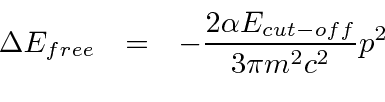
We automatically account for this correction by a change in the observed mass of the electron. For the non-relativistic definition of the energy of a free electron, an increase in the mass decreases the energy.
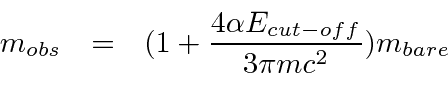
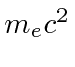 , the correction to the mass is only about 0.3%,
, the correction to the mass is only about 0.3%,
Since the observed mass of the electron already accounts for most of the self energy correction for a bound state, we must correct for this effect to avoid double counting of the correction. The self energy correction for a bound state then is.
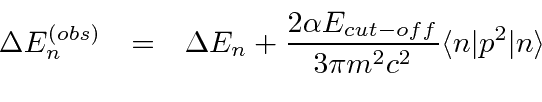
In 1947, Willis E. Lamb and R. C. Retherford used microwave techniques to determine the
splitting between the 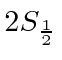 and
and 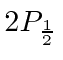 states in Hydrogen.
The result can be well accounted for by the self energy correction, at least when relativistic quantum mechanics is used.
Our non-relativistic calculation gives a qualitative explanation of the effect.
states in Hydrogen.
The result can be well accounted for by the self energy correction, at least when relativistic quantum mechanics is used.
Our non-relativistic calculation gives a qualitative explanation of the effect.
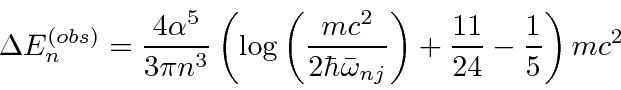
Jim Branson 2013-04-22