Next: Electron Self Energy Up: Course Summary Previous: Quantization of the EM Contents
To scatter a photon the field must act twice,
once to annihilate the initial state photon and once to create the final state photon.
Since the quantized field contains both creation and annihilation operators,
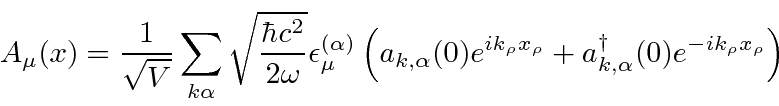
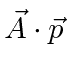 term in second order can contribute to scattering.
Both of these amplitudes are of order
term in second order can contribute to scattering.
Both of these amplitudes are of order
The matrix element of the
![]() term to go from a photon of wave vector
term to go from a photon of wave vector
![]() and an atomic state
and an atomic state
![]() to a
scattered photon of wave vector
to a
scattered photon of wave vector
![]() and an atomic state
and an atomic state
![]() is particularly simple since it contains
no atomic coordinates or momenta.
is particularly simple since it contains
no atomic coordinates or momenta.
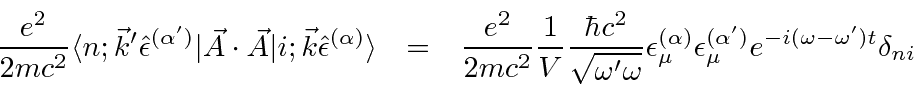
The cross section for photon scattering is then given by the
![\begin{displaymath}\bgroup\color{black} {d\sigma\over d\Omega}
= \left({e^2\over...
...angle
\over \omega_{ji}+\omega'}
\right] \right\vert^2 \egroup\end{displaymath}](img464.png)
This result can be specialized for the case of elastic scattering, with the help of some commutators.
![\begin{displaymath}\bgroup\color{black} {d\sigma_{elas}\over d\Omega}
=\left({e^...
...rangle
\over \omega_{ji}+\omega}
\right] \right\vert^2 \egroup\end{displaymath}](img465.png)
Lord Rayleigh calculated low energy elastic scattering of light from atoms using classical electromagnetism.
If the energy of the scattered photon is less than the energy needed to excite the atom,
then the cross section is proportional to
![]() , so that blue light scatters more than red light does in the
colorless gasses in our atmosphere.
, so that blue light scatters more than red light does in the
colorless gasses in our atmosphere.
If the energy of the scattered photon is much bigger than the binding energy of the atom,
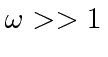 eV.
then the cross section approaches that for scattering from a free electron, Thomson Scattering.
eV.
then the cross section approaches that for scattering from a free electron, Thomson Scattering.
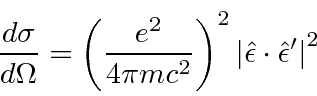
Jim Branson 2013-04-22