Next: Scattering of Photons Up: Course Summary Previous: The Classical Electromagnetic Field Contents
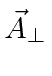 while static charges give rise to
while static charges give rise to
We decompose the radiation field into its Fourier components
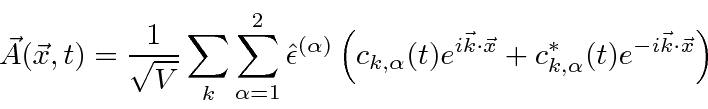
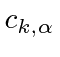 is the coefficient of the wave with wave vector
is the coefficient of the wave with wave vector
Plugging the Fourier decomposition into the formula for the Hamiltonian density and using the transverse nature of the radiation field, we can compute the Hamiltonian (density integrated over volume).
![\begin{eqnarray*}
H&=&\sum\limits_{k,\alpha}\left({\omega\over c}\right)^2
\left...
...(t)c_{k,\alpha}^*(t)+c_{k,\alpha}^*(t)c_{k,\alpha}(t)\right] \\
\end{eqnarray*}](img441.png)
The canonical coordinate and momenta may be found
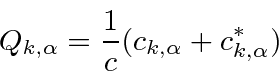
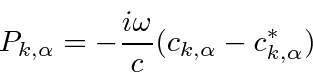
![\begin{eqnarray*}
\left[Q_{k,\alpha},P_{k',\alpha'}\right]&=&i\hbar\delta_{kk'}\...
...\right]&=&0 \\
\left[P_{k,\alpha},P_{k',\alpha'}\right]&=&0 \\
\end{eqnarray*}](img444.png)
As was done for the 1D harmonic oscillator, we write the Hamiltonian in terms of raising and lowering operators that have the same commutation relations as in the 1D harmonic oscillator.
![\begin{eqnarray*}
a_{k,\alpha}&=&{1\over\sqrt{2\hbar\omega}}(\omega Q_{k,\alpha}...
...\alpha'}^\dagger\right]&=&\delta_{kk'}\delta_{\alpha\alpha'} \\
\end{eqnarray*}](img445.png)
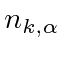 .
.
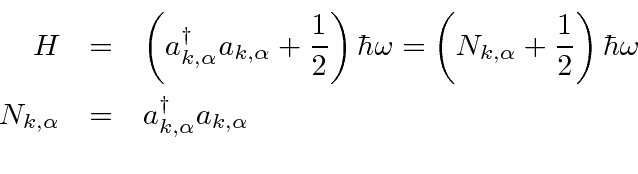
The Fourier coefficients can now be written in terms of the raising and lowering operators for the field.

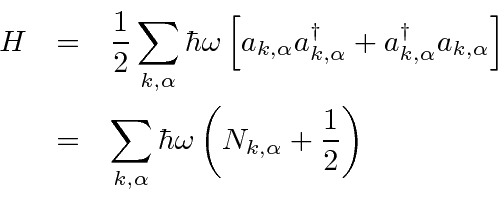
States of the field are given by the occupation number of each possible photon state.
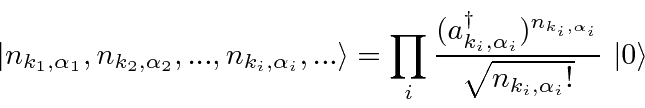
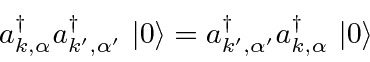
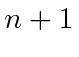 in the emission operator.
in the emission operator.
We can now write the quantized radiation field in terms of the operators at
![]() .
.
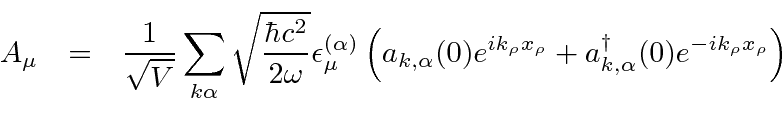
Beyond the Electric Dipole approximation, the next term in the expansion of
![]() is
is
![]() .
This term gets split according to its rotation and Lorentz transformation properties into the Electric Quadrupole term
and the Magnetic Dipole term.
The interaction of the electron spin with the magnetic field is of the same order and should be included
together with the E2 and M1 terms.
.
This term gets split according to its rotation and Lorentz transformation properties into the Electric Quadrupole term
and the Magnetic Dipole term.
The interaction of the electron spin with the magnetic field is of the same order and should be included
together with the E2 and M1 terms.
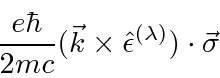
The Electric Quadrupole (E2) term does not change parity and gives us the selection rule.
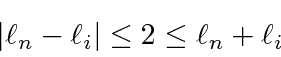
The Magnetic Dipole term (M1) does not change parity but may change the spin. Since it is an (axial) vector operator, it changes angular momentum by 0, +1, or -1 unit.
The quantized field is very helpful in the derivation of Plank's black body radiation formula that started the quantum revolution.
By balancing the reaction rates proportional to
![]() and
and
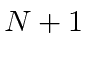 for absorption and emission in equilibrium the energy density
in the radiation field inside a cavity is easily derived.
for absorption and emission in equilibrium the energy density
in the radiation field inside a cavity is easily derived.
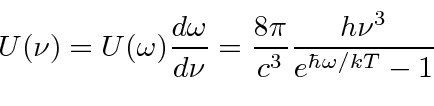
Jim Branson 2013-04-22