Next: Examples Up: Addition of Angular Momentum Previous: General Addition of Angular Contents
If we are combining the angular momentum from two identical particles, like two electrons
in an atom, we will be interested in the symmetry under interchange of the angular momentum
state.
Lets use the combination of two spin
![]() particles as an example.
We know that we get total spin states of
particles as an example.
We know that we get total spin states of
![]() and
and
![]() .
The
.
The
![]() state is called a triplet because there are
three states with different
state is called a triplet because there are
three states with different
![]() values.
The
values.
The
![]() state is called a singlet.The triplet state is symmetric under interchange.
The highest total angular momentum state,
state is called a singlet.The triplet state is symmetric under interchange.
The highest total angular momentum state,
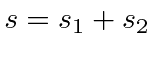 , will always be
symmetric under interchange.We can see this by looking at the highest
, will always be
symmetric under interchange.We can see this by looking at the highest
![]() state,
state,
![]() .
To get the maximum
.
To get the maximum
![]() , both spins to have the maximum
, both spins to have the maximum
![]() component.
So the product state has just one term and it is symmetric under interchange, in this case,
component.
So the product state has just one term and it is symmetric under interchange, in this case,
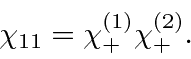
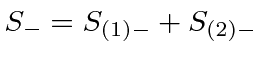 ,
the result remains symmetric under interchange.
To make the next highest state, with two terms,
we must choose a state orthogonal to the
symmetric state and this will always be antisymmetric.
,
the result remains symmetric under interchange.
To make the next highest state, with two terms,
we must choose a state orthogonal to the
symmetric state and this will always be antisymmetric.
In fact, for identical particles, the
symmetry of the angular momentum wave function will alternate,
beginning with a symmetric state for the maximum total angular momentum.
For example, if we add two spin 2 states together, the resulting states are:
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() .
In the language of group theory,
when we take the direct product of two representations of the the SU(2) group we get:
.
In the language of group theory,
when we take the direct product of two representations of the the SU(2) group we get:
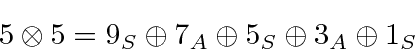
* Example:
Two electrons in a P state.*
* Example:
The parity of the pion from ![]() .*
.*
Jim Branson 2013-04-22