Next: Derivations and Computations Up: Examples Previous: Two electrons in an Contents
We can determine the internal parity of the pion by studying pion capture by a deuteron,
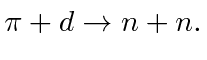 The pion is known to have spin 0, the deuteron spin 1, and the neutron spin
The pion is known to have spin 0, the deuteron spin 1, and the neutron spin
![]() .
The internal parity of the deuteron is +1.
The pion is captured by the deuteron from a 1S states, implying
.
The internal parity of the deuteron is +1.
The pion is captured by the deuteron from a 1S states, implying
![]() in the initial state.
So the total angular momentum quantum number of the initial state is
in the initial state.
So the total angular momentum quantum number of the initial state is
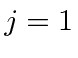 .
.
So the parity of the initial state is
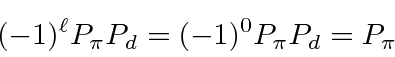
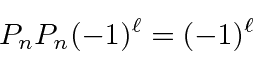
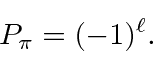
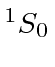 ,
,
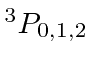 ,
,
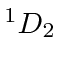 ,
,
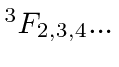 The only state with
The only state with
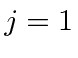 is the
is the
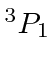 state, so
state, so
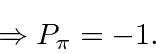
Jim Branson 2013-04-22