Next: The parity of the Up: Examples Previous: Adding to Contents
If we have two atomic electrons in a P state with no external fields applied, states of definite total angular momentum will be the energy eigenstates. We will learn later that closed shells in atoms (or nuclei) have a total angular momentum of zero, allowing us to treat only the valence electrons. Examples of atoms like this would be Carbon, Silicon, and Germanium.
Our two electrons each have
![]() (P state) and
(P state) and
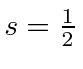 (electrons).
We need to add four angluar momenta together to get the total.
(electrons).
We need to add four angluar momenta together to get the total.
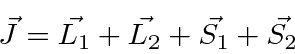
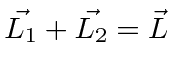 and
and
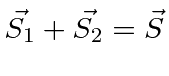 then to add these results
then to add these results
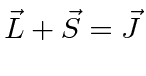 .
.
Since the electrons are identical particles and they are in the same radial state, the angular momentum part of the wavefunction must be antisymmetric under interchange. This will limit the allowed states. So let's do the spinor arithmetic.
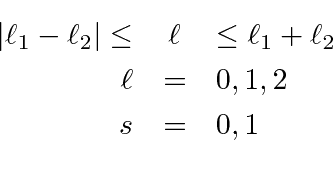
These states have a definite symmetry under interchange.
Before going on to make the total angular momentum states, lets note the symmetry of each of the above states.
The maximum allowed state will always need to be symmetric in order to achieve the maximum.
The symmetry will alternate as we go down in the quantum number.
So, for example, the
![]() and
and
![]() states are symmetric, while the
states are symmetric, while the
![]() state is antisymmetric.
The
state is antisymmetric.
The
![]() state is symmetric and the
state is symmetric and the
![]() state is antisymmetric.
The overall symmetry of a state will be a product of the these two symmetries
(since when we add
state is antisymmetric.
The overall symmetry of a state will be a product of the these two symmetries
(since when we add
![]() and
and
![]() to give
to give
![]() we are not adding identical things anymore).
The overall state must be antisymmetic so we can use:
we are not adding identical things anymore).
The overall state must be antisymmetic so we can use:
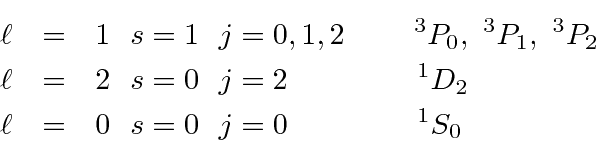
Each atomic state will have the angular momentum quantum numbers
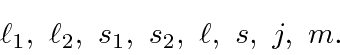
In the atomic physics section, we will even deal with more than two electrons outside a closed shell.
Jim Branson 2013-04-22