Adding to

Adding $\bgroup\color{black}$\ell=4$\egroup$ to $\bgroup\color{black}$\ell=2$\egroup$

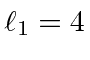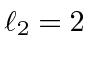As an example, we count the states for each value of total m (z component quantum number) if we add $\bgroup\color{black}$\ell_1 =4$\egroup$ to $\bgroup\color{black}$\ell_2 =2$\egroup$ .

audio

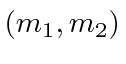Total $\bgroup\color{black}$m$\egroup$	$\bgroup\color{black}$(m_1,m_2)$\egroup$
6	(4,2)
5	(3,2) (4,1)
4	(2,2) (3,1) (4,0)
3	(1,2) (2,1) (3,0) (4,-1)
2	(0,2) (1,1) (2,0) (3,-1) (4,-2)
1	(-1,2) (0,1) (1,0) (2,-1) (3,-2)
0	(-2,2) (-1,1) (0,0) (1,-1) (2,-2)
-1	(1,-2) (0,-1) (-1,0) (-2,1) (-3,2)
-2	(0,-2) (-1,-1) (-2,0) (-3,1) (-4,2)
-3	(-1,-2) (-2,-1) (-3,0) (-4,1)
-4	(-2,-2) (-3,-1) (-4,0)
-5	(-3,-2) (-4,-1)
-6	(-4,-2)

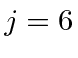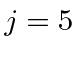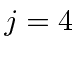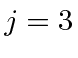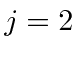Since the highest m value is 6, we expect to have a $\bgroup\color{black}$j=6$\egroup$ state which uses up one state for each m value from -6 to +6. Now the highest m value left is 5, so a $\bgroup\color{black}$j=5$\egroup$ states uses up a state at each m value between -5 and +5. Similarly we find a $\bgroup\color{black}$j=4$\egroup$ , $\bgroup\color{black}$j=3$\egroup$ , and $\bgroup\color{black}$j=2$\egroup$ state. This uses up all the states, and uses up the states at each value of m. So we find in this case,

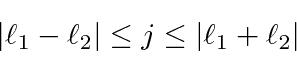
$\begin{displaymath}\bgroup\color{black} \vert\ell_1 - \ell_2\vert\leq j \leq \vert\ell_1 + \ell_2\vert \egroup\end{displaymath}$

and that $\bgroup\color{black}$j$\egroup$ takes on every integer value between the limits. This makes sense in the vector model.

Jim Branson 2013-04-22