Next: Interchange Symmetry for States Up: Addition of Angular Momentum Previous: Spectroscopic Notation Contents
We have already worked several examples of addition of angular momentum. Lets work one more.
* Example:
Adding ![]() to
to ![]() .*
.*
The result, in agreement with our classical vector model, is multiplets with
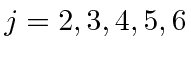 .
.
The vector model qualitatively explains the limits.
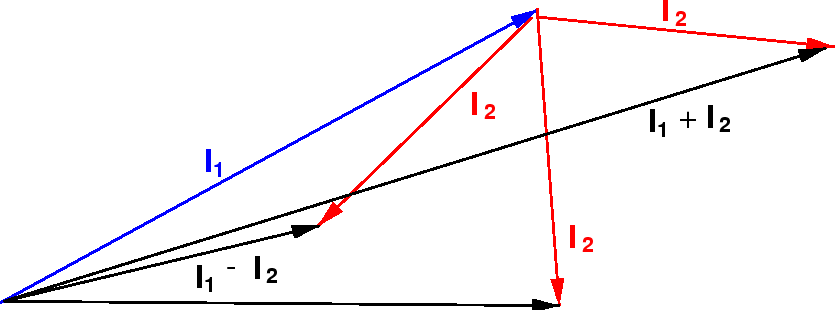
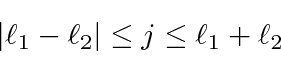
We can check that the number of states agrees with the number of product states.
We have been expanding the states of definite total angular momentum
![]() in terms of the
product states for several cases.
The general expansion is called the Clebsch-Gordan series:
in terms of the
product states for several cases.
The general expansion is called the Clebsch-Gordan series:
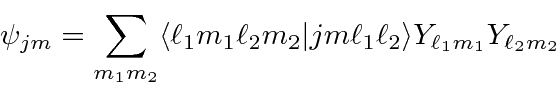
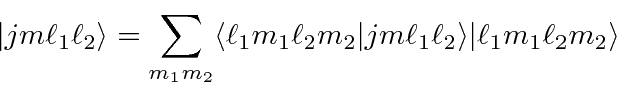
Jim Branson 2013-04-22