Next: Spectroscopic Notation Up: Addition of Angular Momentum Previous: Total Angular Momentum and Contents
Our goal is to add orbital angular momentum with quantum number
![]() to spin
to spin
![]() .
We can show in several ways that, for
.
We can show in several ways that, for
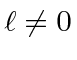 , that the total angular momentum quantum
number has two possible values
, that the total angular momentum quantum
number has two possible values
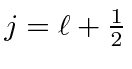 or
or
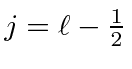 .For
.For
![]() , only
, only
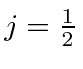 is allowed.
First lets argue that this makes sense when we are adding two vectors. For example
if we add a vector of length 3 to a vector of length 0.5, the resulting
vector could take on a length between 2.5 and 3.5
For quantized angular momentum, we will only have the half integers allowed, rather
than a continuous range.
Also we know that the quantum numbers like
is allowed.
First lets argue that this makes sense when we are adding two vectors. For example
if we add a vector of length 3 to a vector of length 0.5, the resulting
vector could take on a length between 2.5 and 3.5
For quantized angular momentum, we will only have the half integers allowed, rather
than a continuous range.
Also we know that the quantum numbers like
![]() are not exactly the length of the
vector but are close.
So these two values make sense physically.
are not exactly the length of the
vector but are close.
So these two values make sense physically.
We can also count states for each eigenvalue of
![]() as in the following examples.
as in the following examples.
* Example:
Counting states for ![]() plus spin
plus spin ![]() .*
.*
* Example:
Counting states for any ![]() plus spin
plus spin ![]() .*
.*
As in the last section, we could start with the highest
![]() state,
state,
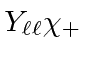 ,
and apply the lowering operator to find the rest of the
multiplet with
,
and apply the lowering operator to find the rest of the
multiplet with
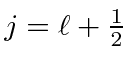 .
This works well for some specific
.
This works well for some specific
![]() but is hard to generalize.
but is hard to generalize.
We can work the problem in general. We know that each eigenstate of
![]() and
and
![]() will be a linear combination of the two product states with the right
will be a linear combination of the two product states with the right
![]() .
.
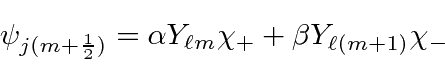
The coefficients
![]() and
and
![]() must be
determined
by operating with
must be
determined
by operating with ![]() .
.
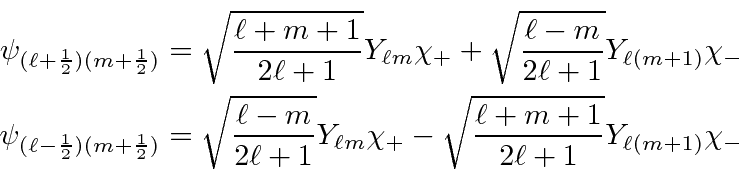
Jim Branson 2013-04-22