Next: Counting states for Arbitrary Up: Examples Previous: Examples Contents
For
![]() there are
there are
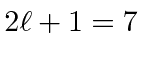 different eigenstates of
different eigenstates of
![]() .
There are two different eigenstates of
.
There are two different eigenstates of
![]() for spin
for spin
![]() .
We can have any combination of these states, implying
.
We can have any combination of these states, implying
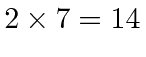 possible product states
like
possible product states
like
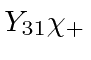 .
.
We will argue based on adding vectors... that there will be two total angular momentum
states that can be made up from the 14 product states,
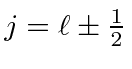 , in this case
, in this case
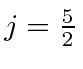 and
and
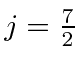 .
Each of these has
.
Each of these has
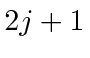 states, that is 6 and 8 states respectively.
Since
states, that is 6 and 8 states respectively.
Since
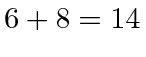 this gives us the right number of states.
this gives us the right number of states.