Next: Counting the States for Up: Derivations and Computations Previous: Applying the Operator to Contents
We wish to write the states of total angular momentum
![]() in terms of the
product states
in terms of the
product states
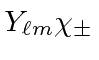 .
We will do this by operating with the
.
We will do this by operating with the
![]() operator and setting the coefficients
so that we have eigenstates.
operator and setting the coefficients
so that we have eigenstates.
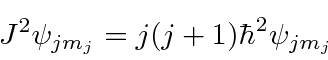
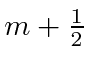 .
This is really just the defintion of the dummy variable
.
This is really just the defintion of the dummy variable
The z component of the total angular momentum is just the sum of the z components from
the orbital and the spin.
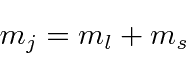
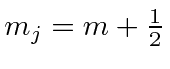 .
If the spin is up we need
.
If the spin is up we need
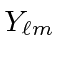 and if the spin is down,
and if the spin is down,
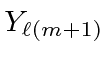 .
.
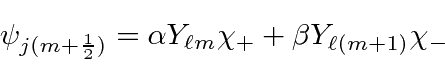
We will find the coefficients
![]() and
and
![]() so that
so that
![]() will be an eigenstate of
will be an eigenstate of
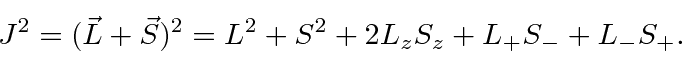
So operate on the right hand side with
![]() .
.
![\begin{eqnarray*}
J^2\psi_{j,m+{1\over 2}}
= &\alpha&\hbar^2\left[\ell(\ell+1)Y...
... \sqrt{\ell(\ell + 1) - (m+1)m} \sqrt{(1)} Y_{lm}\chi_+ \right]
\end{eqnarray*}](img2887.png)
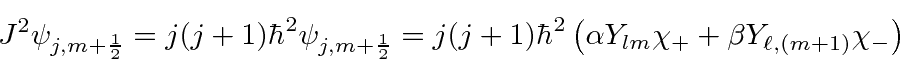
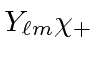 term gives
term gives
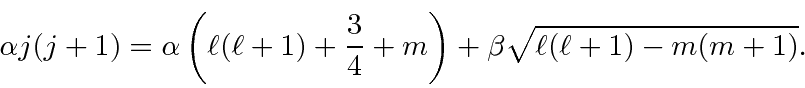
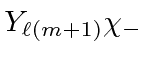 term gives
term gives
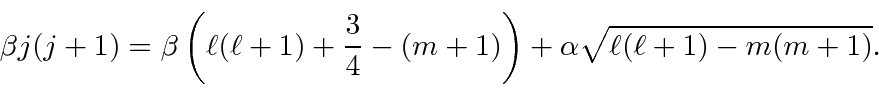
![\begin{eqnarray*}
\left(j(j+1)-\ell(\ell + 1)-{3\over 4}-m\right)\alpha
&=& \sq...
...a
&=& \left[j(j+1)-\ell(\ell + 1)-{3\over 4}+(m+1)\right]\beta
\end{eqnarray*}](img2893.png)
Now we just cross multiply so we have one equation with a common factor of
![]() .
.
![\begin{displaymath}\bgroup\color{black}(\ell-m)(\ell+m+1)=\left[j(j+1)-\ell(\ell...
...ght]
\left[j(j+1)-\ell(\ell+1)-{3\over 4}+(m+1)\right] \egroup\end{displaymath}](img2895.png)
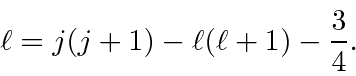
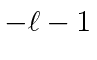 .
.
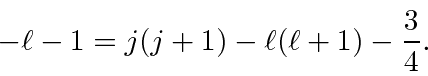
These are now simple to solve
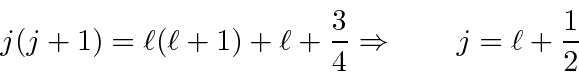
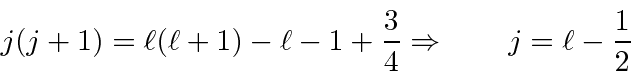
Plugging
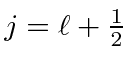 into our first equation,
into our first equation,
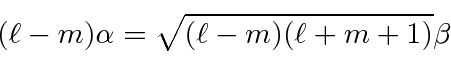
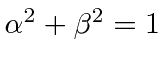 .
So lets get the squares.
.
So lets get the squares.
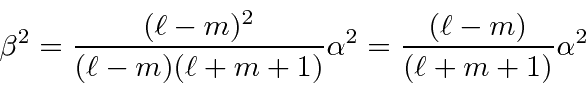
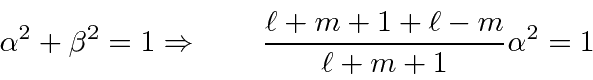
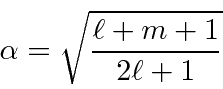
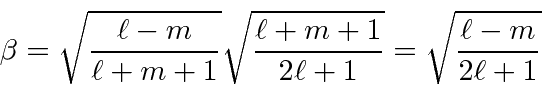
So we have completed the calculation of the coefficients. We will make use of these in the hydrogen atom, particularly for the anomalous Zeeman effect.
Writing this in the
notation of matrix elements or Clebsch-Gordan coefficients of the form,
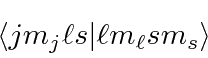
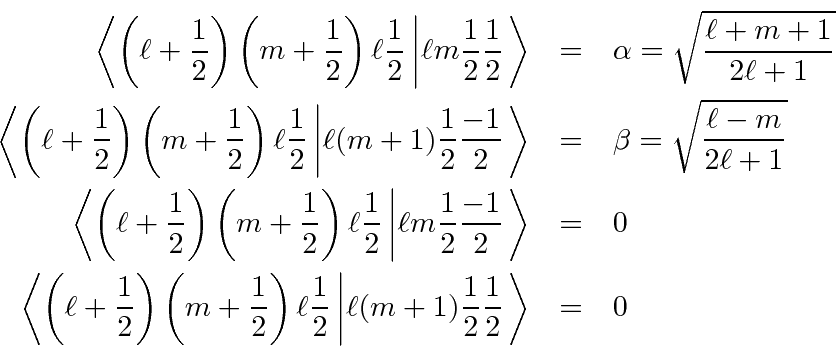
Similarly
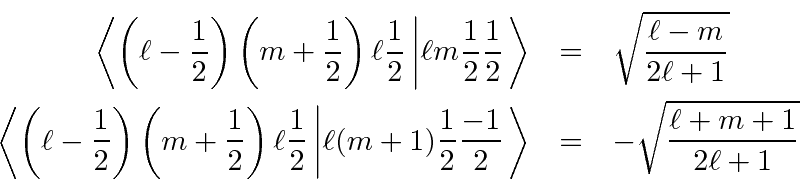
Jim Branson 2013-04-22