Next: Quantum Mechanics in an Up: Course Summary Previous: A Study of Operators Contents
The angular momentum algebra defined by the commutation relations between the operators requires that the total angular momentum quantum number must either be an integer or a half integer. The half integer possibility was not useful for orbital angular momentum because there was no corresponding (single valued) spherical harmonic function to represent the amplitude for a particle to be at some position.
The half integer possibility is used to represent the internal angular momentum of some particles.
The simplest and most important case is
spin one-half.
There are just two possible states with different z components of spin:
spin up
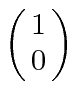 , with z component of angular momentum
, with z component of angular momentum
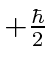 , and
spin down
, and
spin down
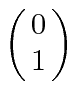 , with
, with
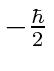 .
The corresponding spin operators are
.
The corresponding spin operators are
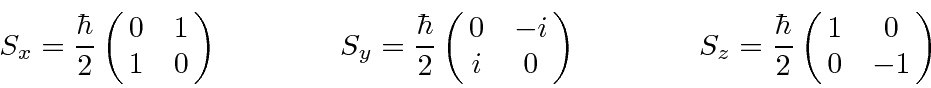
It is common to define the Pauli Matrices,
![]() , which have the following properties.
, which have the following properties.
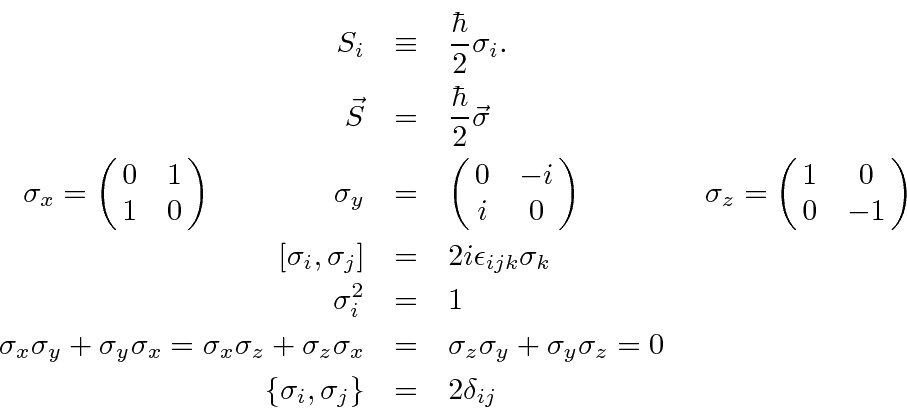
Jim Branson 2013-04-22