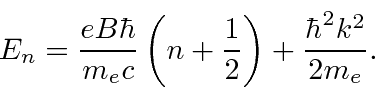The classical Hamiltonian for a particle in an Electromagnetic field is
where
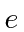 is defined to be a positive number.
This Hamiltonian gives the correct Lorentz force law.
Note that the momentum operator will now include momentum in the field, not just the particle's momentum.
As this Hamiltonian is written,
is defined to be a positive number.
This Hamiltonian gives the correct Lorentz force law.
Note that the momentum operator will now include momentum in the field, not just the particle's momentum.
As this Hamiltonian is written,
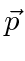 is the variable conjugate to
is the variable conjugate to
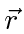 and is related to the velocity by
and is related to the velocity by
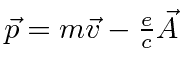 .
.
In Quantum Mechanics,
the momentum operator is replaced
in the same way to include the effects of magnetic fields and eventually radiation.
Starting from the above Hamiltonian, we derive the
Hamiltonian for a particle in a constant magnetic field.
This has the familiar effect of a magnetic moment parallel to the angular momentum vector,
plus some additional terms which are very small for atoms in fields realizable in the laboratory.
So, for atoms, the dominant additional term is
where
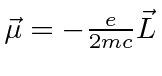 .
This is, effectively, the magnetic moment
due to the electron's orbital angular momentum.
.
This is, effectively, the magnetic moment
due to the electron's orbital angular momentum.
The other terms can be important if a state is spread over a region much larger than an atom.
We work the example of a plasma in a constant magnetic field.
A charged particle in the plasma has the following energy spectrum
which depends on 2 quantum numbers.
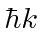 is the conserved momentum along the field direction which
can take on any value.
is the conserved momentum along the field direction which
can take on any value.
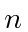 is an integer dealing with the state in x and y.
This problem can be simplified using a few different symmetry operators.
We work it two different ways: in one it reduces to the radial equation for the Hydrogen atom;
in the other it reduces to the Harmonic Oscillator equation,
showing that these two problems we can solve are somehow equivalent.
is an integer dealing with the state in x and y.
This problem can be simplified using a few different symmetry operators.
We work it two different ways: in one it reduces to the radial equation for the Hydrogen atom;
in the other it reduces to the Harmonic Oscillator equation,
showing that these two problems we can solve are somehow equivalent.
Jim Branson
2013-04-22
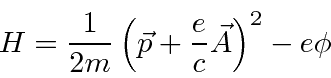
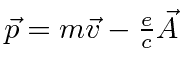 .
.
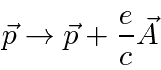
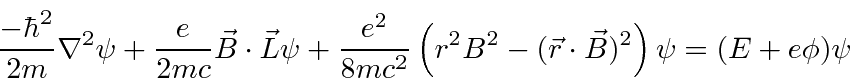
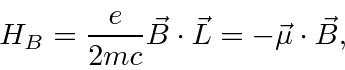
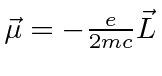 .
This is, effectively, the magnetic moment
due to the electron's orbital angular momentum.
.
This is, effectively, the magnetic moment
due to the electron's orbital angular momentum.