Next: Spin 1/2 and other Up: Course Summary Previous: Matrix Representation of Operators Contents
The set of states with the same total angular momentum and the angular momentum operators which
act on them are often represented by vectors and matrices.
For example the different
![]() states for
states for
![]() will be represented by a 3 component vector
and the
angular momentum operators
represented by 3X3 matrices.
There are both practical and theoretical reasons why this set of states is separated from the states
with different total angular momentum quantum numbers.
The states are often (nearly) degenerate and therefore should be treated as a group for practical reasons.
Also, a rotation of the coordinate axes will not change the total angular momentum quantum number so
the rotation operator works within this group of states.
will be represented by a 3 component vector
and the
angular momentum operators
represented by 3X3 matrices.
There are both practical and theoretical reasons why this set of states is separated from the states
with different total angular momentum quantum numbers.
The states are often (nearly) degenerate and therefore should be treated as a group for practical reasons.
Also, a rotation of the coordinate axes will not change the total angular momentum quantum number so
the rotation operator works within this group of states.
We write our 3 component vectors as follows.
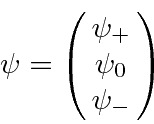
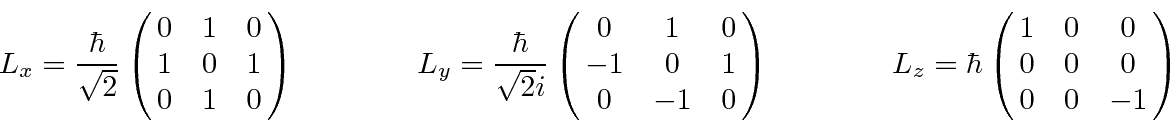
The rotation operators (symmetry operators) are given by
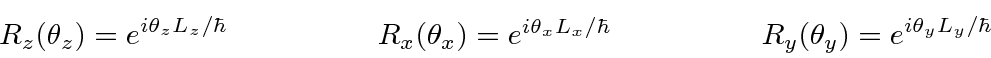
Jim Branson 2013-04-22