Next: Derivations and Computations Up: Wave Packets Previous: Position Space and Momentum Contents
So far, we have performed our Fourier Transforms at
![]() and looked at the result only at
and looked at the result only at
![]() .
We will now put time back into the wave function
and look at the wave packet at later times.
We will see that the behavior of photons and non-relativistic electrons is quite different.
.
We will now put time back into the wave function
and look at the wave packet at later times.
We will see that the behavior of photons and non-relativistic electrons is quite different.
Assume we start with our Gaussian (minimum uncertainty) wavepacket
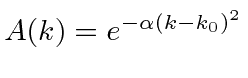 at
at
![]() .
We can do the Fourier Transform to position space, including the time dependence.
.
We can do the Fourier Transform to position space, including the time dependence.
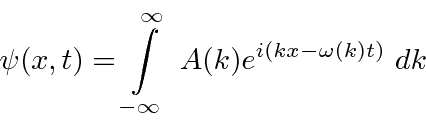
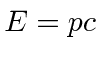 , so
, so
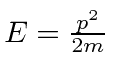 , so
, so
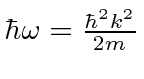 ,
and hence
,
and hence
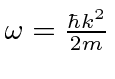 .
.
To cover the general case, lets expand
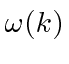 around the center of the wave packet in k-space.
around the center of the wave packet in k-space.
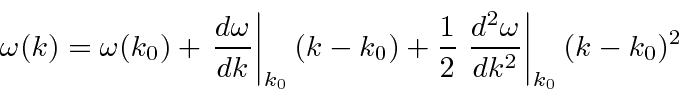
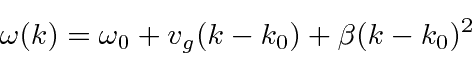
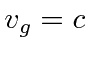 and
and
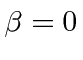 .
For the NR electron,
.
For the NR electron,
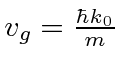 and
and
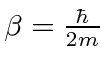 .
.
Performing the Fourier Transform, we get
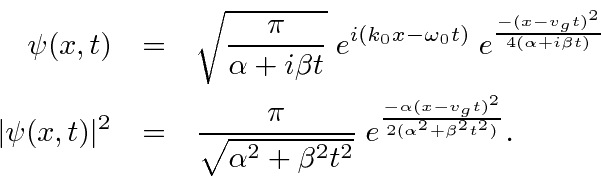
We see that the photon will move with the velocity of light and that the wave packet will not disperse,
because
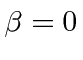 .
.
For the NR electron, the wave packet moves with the correct group velocity,
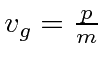 ,
but the wave packet spreads with time.
The RMS width is
,
but the wave packet spreads with time.
The RMS width is
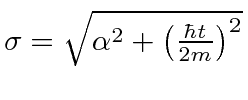 .
.
A wave packet naturally spreads because it contains waves of different momenta and hence different velocities. Wave packets that are very localized in space spread rapidly.
Jim Branson 2013-04-22