Next: Numbers Up: Derivations and Computations Previous: Fourier Transform of Gaussian Contents
Assume we start with our Gaussian (minimum uncertainty) wavepacket
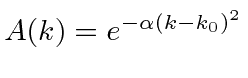 at
at
![]() .
We are not interested in careful normalization here so we will drop constants.
.
We are not interested in careful normalization here so we will drop constants.
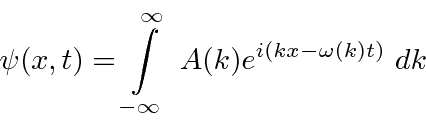
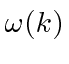 around the center of the wave packet in k-space.
around the center of the wave packet in k-space.
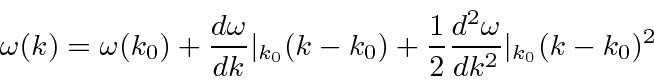
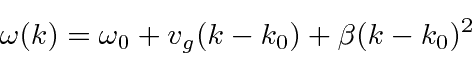
We still need to do the integral as before.
Make the substitution
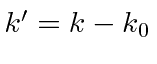 giving
giving
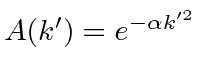 .
Factor out the constant exponential that has no
.
Factor out the constant exponential that has no
![]() dependence.
dependence.
![\begin{eqnarray*}
\psi(x,t)&=&e^{i(k_0x-w_0t)}\; \int\limits_{-\infty}^\infty\; ...
...y}^\infty\; e^{-[\alpha-i\beta t] k'^2} e^{i(k'x-v_gt)}\; dk'\\
\end{eqnarray*}](img894.png)
We now compare this integral to the one we did earlier (so we can avoid the work of completing the square again).
Dropping the constants, we had
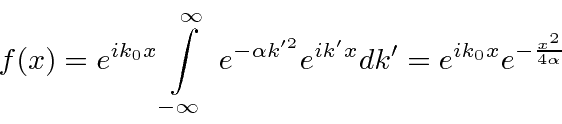
Our new integral is the same with the substitutions
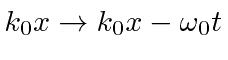 ,
,
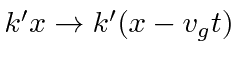 ,
and
,
and
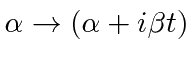 .
We can then write down the answer
.
We can then write down the answer
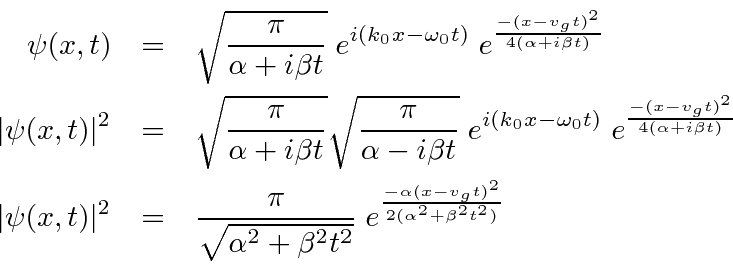
Jim Branson 2013-04-22