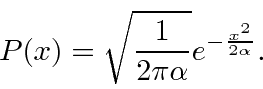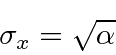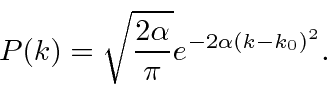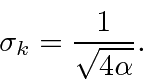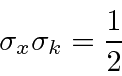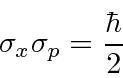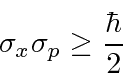Fourier Transform of Gaussian *
We wish to Fourier transform the Gaussian wave packet in (momentum) k-space
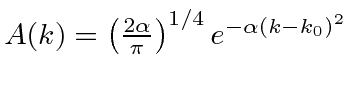 to get
to get
 in position space.
The Fourier Transform formula is
in position space.
The Fourier Transform formula is
Now we will transform the integral a few times to get to the standard definite integral of
a Gaussian for which we know the answer.
First,
which does nothing really since
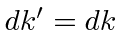 .
.
Now we want to complete the square in the exponent inside the integral.
We plan a term like
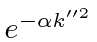 so we define
so we define
Again
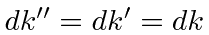 .
Lets write out the planned exponent to see what we are missing.
.
Lets write out the planned exponent to see what we are missing.
We need to multiply by
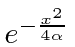 to cancel the extra term in the completed square.
to cancel the extra term in the completed square.
That term can be pulled outside the integral since it doesn't depend on
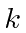 .
.
So now we have the standard Gaussian integral which just gives us
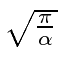 .
.
Lets check the normalization.
Given a normalized
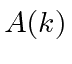 , we get a normalized
, we get a normalized
 .
.
The RMS deviation, or standard deviation of a Gaussian can be read from the distribution.
Squaring
 , we get
, we get
Reading from either the coefficient or the exponential we see that
For the width in k-space,
Reading from the coefficient of the exponential, we get
We can see that as we vary the width in k-space, the width in x-space varies to keep the product constant.
Translating this into momentum, we get the limit of the Heisenberg Uncertainty Principle.
In fact the Uncertainty Principle states that
so the Gaussian wave packets seem to saturate the bound!
Jim Branson
2013-04-22
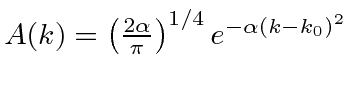 to get
to get
 in position space.
The Fourier Transform formula is
in position space.
The Fourier Transform formula is
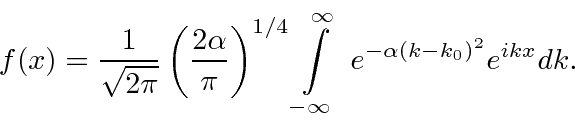
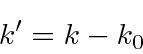
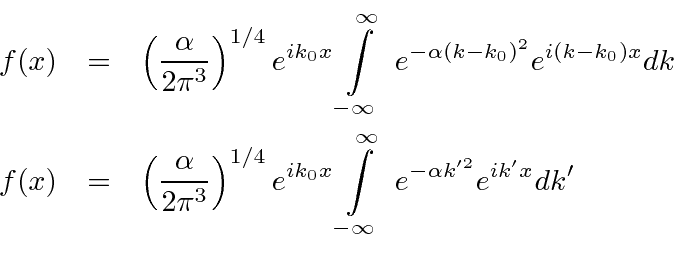
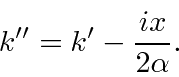
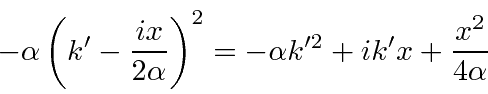
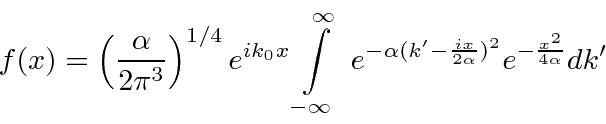
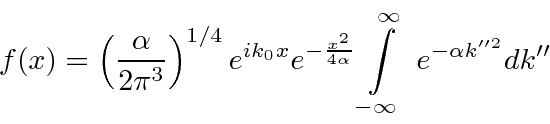
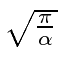 .
.
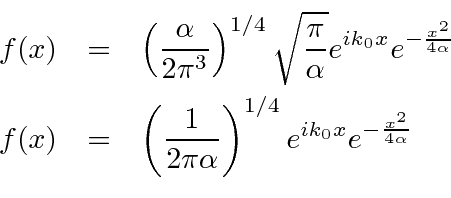
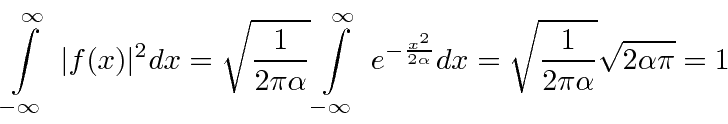
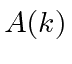 , we get a normalized
, we get a normalized
 .
.
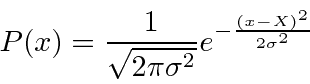
 , we get
, we get