Next: Time Development of a Up: Wave Packets Previous: The Heisenberg Uncertainty Principle Contents
We can represent a state with either
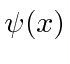 or with
or with
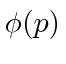 .
We can (Fourier) transform from one to the other.
.
We can (Fourier) transform from one to the other.
We have the symmetric Fourier Transform.
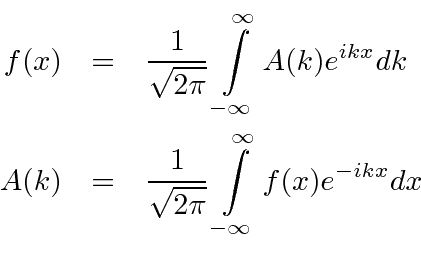
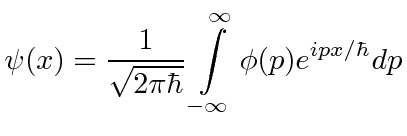
|
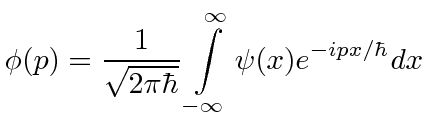 |
These formulas are worth a little study.
If we define
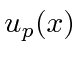 to be the state with definite momentum
to be the state with definite momentum
![]() , (in position space)
our formula for it is
, (in position space)
our formula for it is
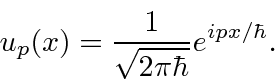
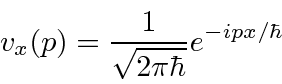
Our Fourier Transform can now be read to say that we add up states of definite momentum to get
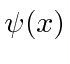
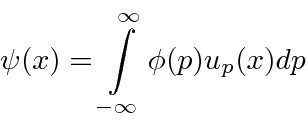
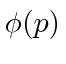 .
.
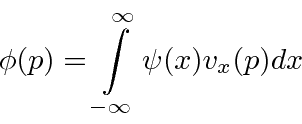
There is a more abstract way to write these states.
Using the notation of Dirac, the state with definite momentum
![]() ,
,
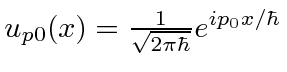 might be written as
might be written as
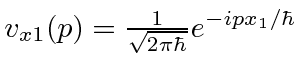 might be written
might be written
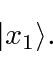
The arbitrary state represented by either
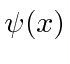 or
or
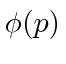 ,
might be written simple as
,
might be written simple as
The actual wave function
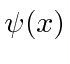 would be written as
would be written as
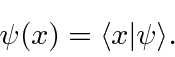
We will find that there are other ways to represent Quantum states. This was a preview. We will spend more time on Dirac Bra-ket notation later.
Jim Branson 2013-04-22