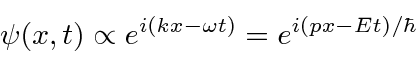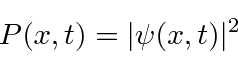The Solution: Probability Amplitudes
For EM waves, the intensity, and hence the probability to find a photon,
is proportional to the square of the fields.
The fields obey the wave equation.
The fields from two slits can add constructively or destructively giving interference patterns.
The
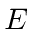 and
and
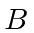 fields are 90 degrees out of phase and both contribute to the intensity.
fields are 90 degrees out of phase and both contribute to the intensity.
We will use the same ideas for electrons, although the details of the field will vary a bit
because electrons and photons are somewhat different kinds of particles.
For both particles the wavelength is given by
and the frequency by
We will use a complex probability amplitude
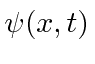 for the electron.
The real and imaginary parts are out of phase like the EM fields.
The traveling wave with momentum
for the electron.
The real and imaginary parts are out of phase like the EM fields.
The traveling wave with momentum
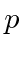 and energy
and energy
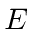 then is
then is
The probability to find an electron is equal to the absolute square of the complex probability amplitude.
(We will overcome the problem that this probability is 1 everywhere for our simple wavefunction.)
We have just put in most of the physics of Quantum Mechanics. Much of what we do for the
rest of the course will be deduced from the paragraph above. Our input came from deBroglie and Plank,
with support from experiments.
Lets summarize the physics input again.
- Free particles are represented by complex wave functions with a relationship between their
particle properties - energy and momentum, and their wave properties - frequency and wavelength
given by Plank and deBroglie.
- The absolute square of the wavefunction gives the probability distribution function.
Quantum Mechanics only tells us the probability.
- We can make superpositions of our free particle wave functions to make states that do not have definite momentum.
We will find that any state can be made from the superposition of free particle states with different momentum.
We now have a wave-particle duality for all the particles, however,
physics now only tells us the probability for some quantum events to occur.
We have lost the complete predictive power of classical physics.
Gasiorowicz Chapter 1
Rohlf Chapter 5
Griffiths 1.2, 1.3
Cohen-Tannoudji et al. Chapter
Subsections
Jim Branson
2013-04-22
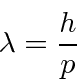
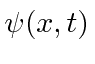 for the electron.
The real and imaginary parts are out of phase like the EM fields.
The traveling wave with momentum
for the electron.
The real and imaginary parts are out of phase like the EM fields.
The traveling wave with momentum