Next: Review of Traveling Waves Up: Derivations and Computations Previous: Derivations and Computations Contents
A complex number
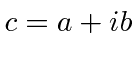 consists of a real part
consists of a real part
![]() and an imaginary part
and an imaginary part
![]() .
(We choose
.
(We choose
![]() and
and
![]() to be real numbers.)
to be real numbers.)
![]() is the square root of -1.
is the square root of -1.
The complex conjugate of
![]() is
is
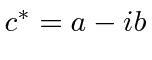 .
(Just change the sign of all the
.
(Just change the sign of all the
![]() .)
.)
The absolute square of a complex number is calculated by multiplying it by its complex conjugate.
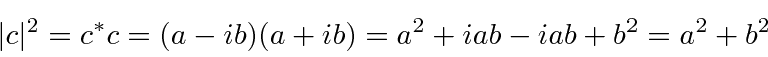
We will use complex exponentials all the time.
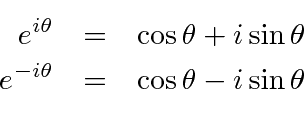
We can write
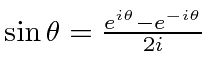 and
and
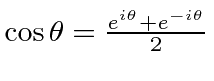 .
.
As with other exponentials, we can multiply them by adding the exponents.
Jim Branson 2013-04-22