Next: Sample Test Problems Up: Derivations and Computations Previous: Review of Complex Numbers Contents
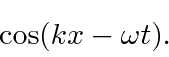
The phase of the wave goes through
![]() in one wavelength in
in one wavelength in
![]() .
So the wavelength
.
So the wavelength
![]() satisfies
satisfies
Similarly the phase goes through
![]() in one period
in one period
![]() in time.
in time.
![]() is the angular frequency. It changes by
is the angular frequency. It changes by
![]() every cycle.
The frequency
every cycle.
The frequency
![]() increases by 1 every cycle so
increases by 1 every cycle so
There is no reason to memorize these equations. They should be obvious.
Lets see how fast one of the peaks of the wave moves. This is called the phase velocity.
At time
![]() , there is a peak at
, there is a peak at
![]() . This is the peak for which the argument of cosine is 0.
At time
. This is the peak for which the argument of cosine is 0.
At time
![]() , the argument is zero when
, the argument is zero when
![]() or at
or at
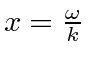 .
If we compute the phase velocity by taking
.
If we compute the phase velocity by taking
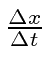 , we get
, we get
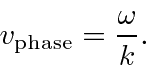
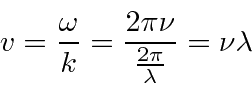
In non-relativistic QM, we have
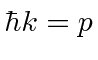 ,
,
![]() , and
, and
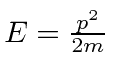 , so
, so
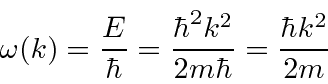
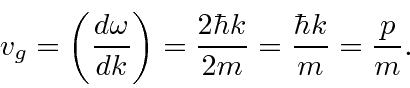
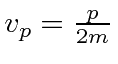 .)
.)
Jim Branson 2013-04-22