Next: Vacuum Polarization Up: Dirac Equation Previous: Quantization of the Dirac Contents
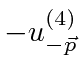 with the positron spinor
with the positron spinor
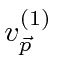 and
and
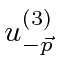 with
with
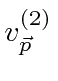 such that the new spinors are charge conjugates of
the electron spinors.
such that the new spinors are charge conjugates of
the electron spinors.
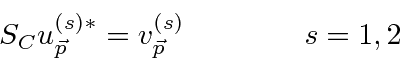
We name the creation and annihilation operators for the positron states to be
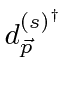 and
and
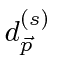 and identify them to be.
and identify them to be.
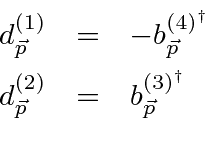
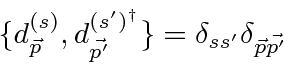
The Dirac field and Hamiltonian can now be rewritten.
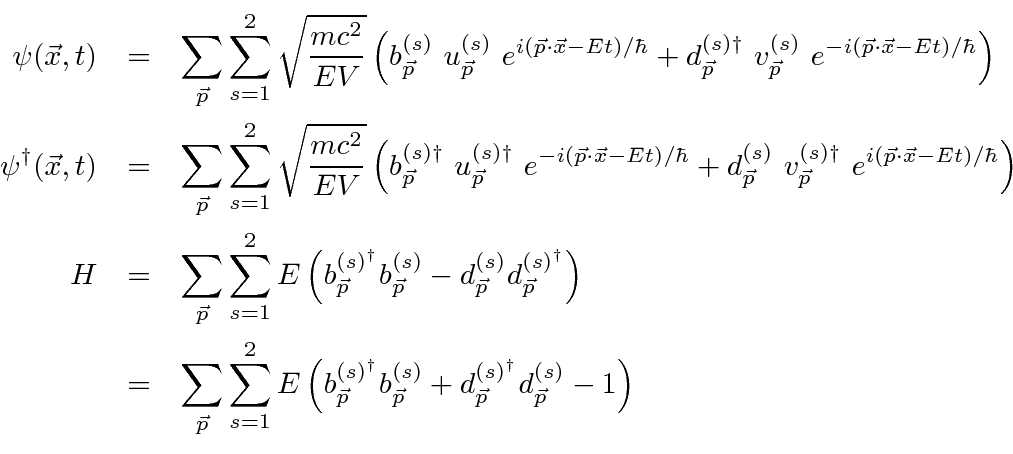
There is an (infinite) constant energy, similar but of opposite sign to the one for the quantized EM field, which we must add to make the vacuum state have zero energy. Note that, had we used commuting operators (Bose-Einstein) instead of anti-commuting, there would have been no lowest energy ground state so this Energy subtraction would not have been possible. Fermi-Dirac statistics are required for particles satisfying the Dirac equation.
Since the operators creating fermion states anti-commute,
fermion states must be antisymmetric under interchange.
Assume
![]() and
and
![]() are the creation and annihilation operators for fermions and that they anti-commute.
are the creation and annihilation operators for fermions and that they anti-commute.
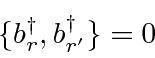
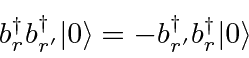
Note that the spinors satisfy the following equations.
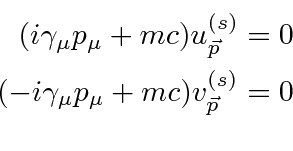
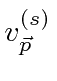 ,
the momentum term in the Dirac equation had to change sign.
,
the momentum term in the Dirac equation had to change sign.
Jim Branson 2013-04-22