Next: The Quantized Dirac Field Up: Dirac Equation Previous: Charge Conjugate Waves Contents

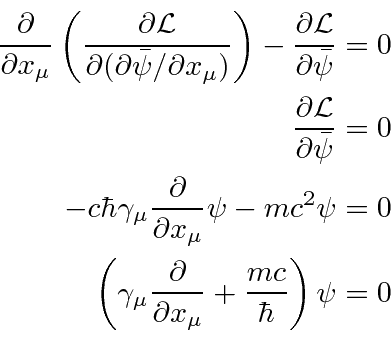
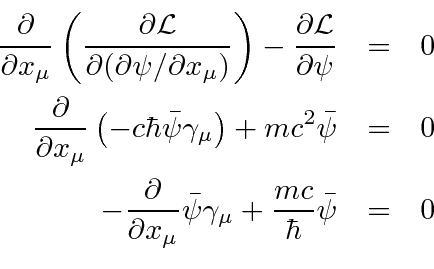
To compute the Hamiltonian density, we start by finding the momenta conjugate to the fields
![]() .
.
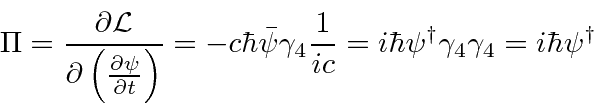
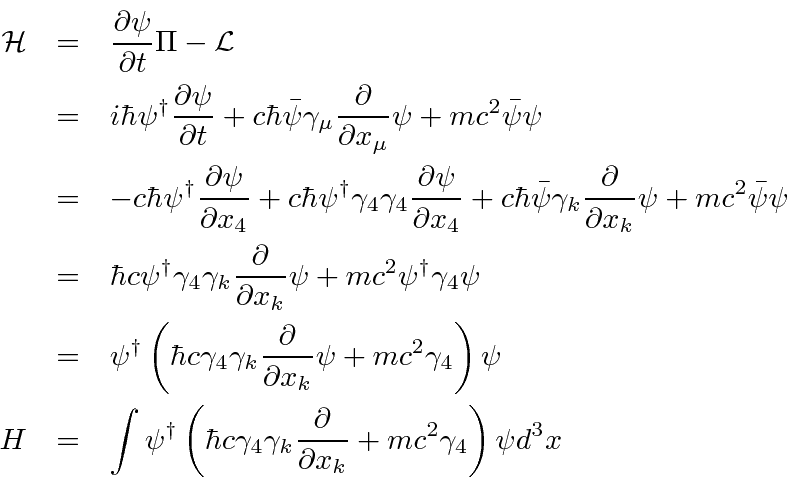
We may expand the field
![]() in the complete set of plane waves
either using the four spinors
in the complete set of plane waves
either using the four spinors
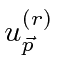 for
for
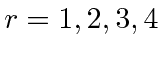 or using the electron and positron spinors
or using the electron and positron spinors
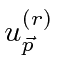 and
and
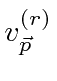 for
for
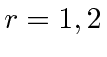 .
For economy of notation, we choose the former with a plan to change to the later once the quantization is completed.
.
For economy of notation, we choose the former with a plan to change to the later once the quantization is completed.
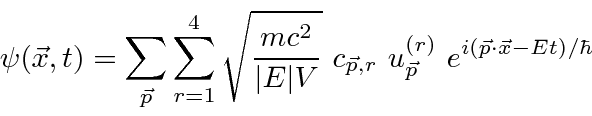
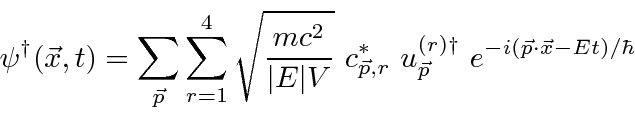
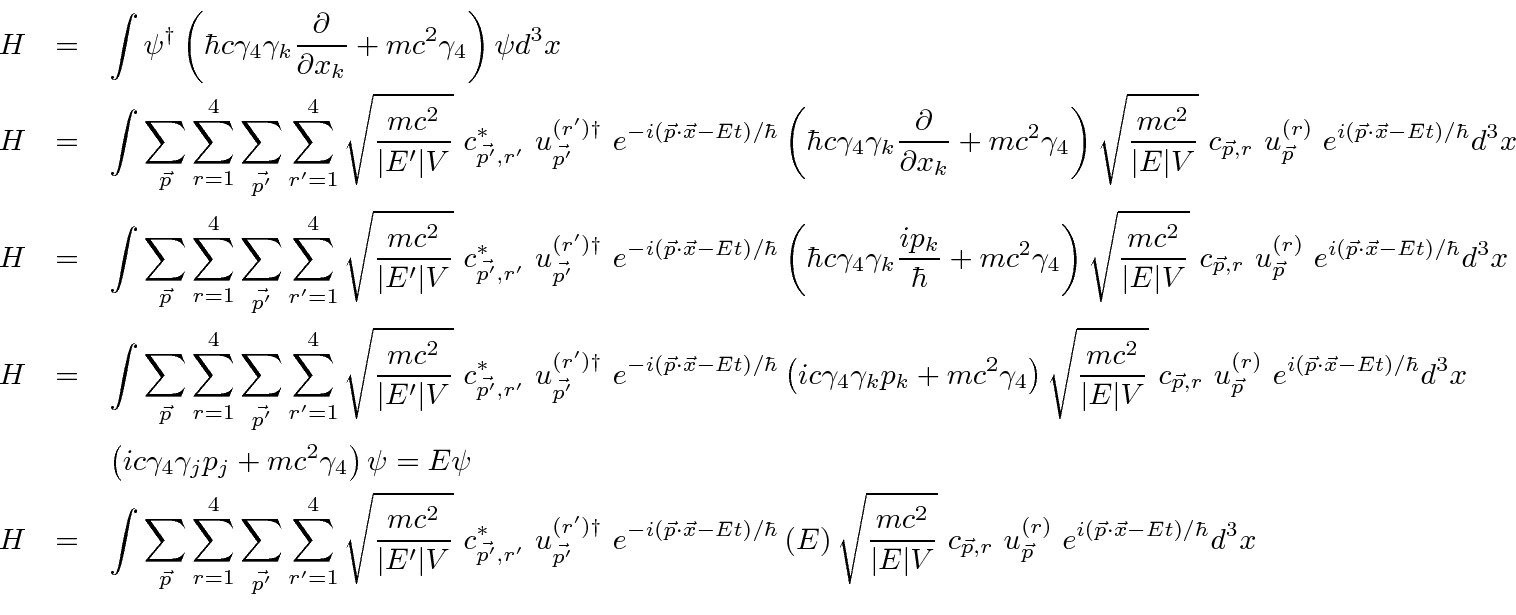
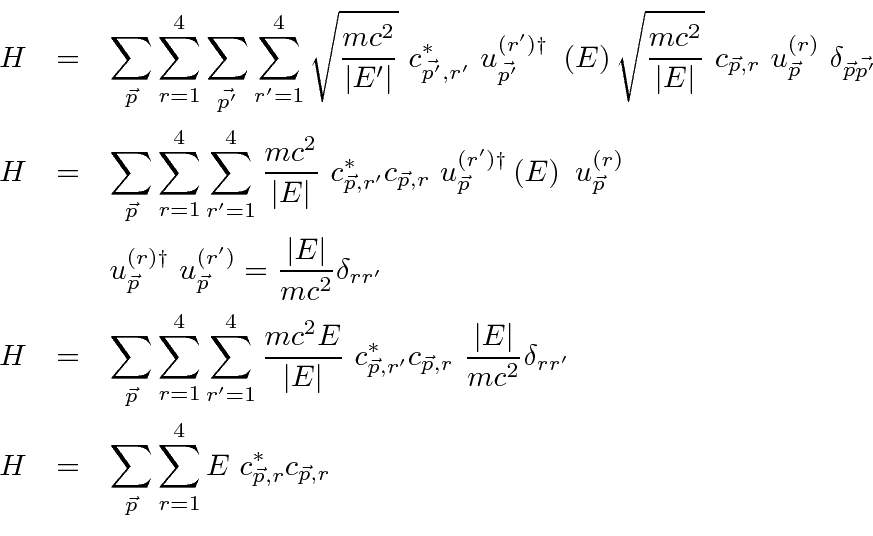
Compare this Hamiltonian to the one used to quantize the Electromagnetic field
![\begin{displaymath}\bgroup\color{black} H=\sum\limits_{k,\alpha}\left({\omega\ov...
...\alpha}c_{k,\alpha}^*+c_{k,\alpha}^*c_{k,\alpha}\right] \egroup\end{displaymath}](img3918.png)
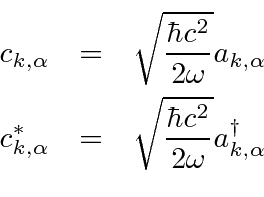
![\begin{eqnarray*}
H&=&{1\over 2}\sum\limits_{k,\alpha}\hbar\omega\left[a_{k,\alp...
..._{k,\alpha}^\dagger+a_{k,\alpha}^\dagger a_{k,\alpha}\right] \\
\end{eqnarray*}](img4526.png)
By analogy, we can skip the steps of making coordinates and momenta for the individual oscillators, and just replace the Fourier coefficients for the Dirac plane waves by operators.
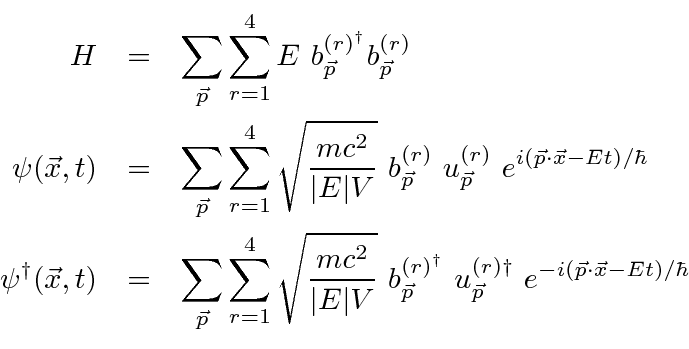
The creation an annihilation operators
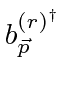 and
and
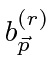 satisfy anticommutation relations.
satisfy anticommutation relations.
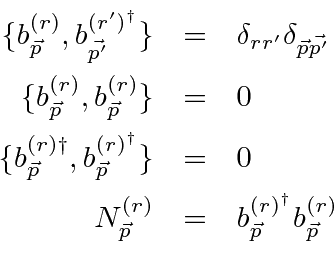
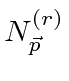 is the occupation number operator.
The anti-commutation relations constrain the occupation number to be 1 or 0.
is the occupation number operator.
The anti-commutation relations constrain the occupation number to be 1 or 0.
A state of the electrons in a system can be described by the occupation numbers (0 or 1 for each plane wave). The state can be generated by operation on the vacuum state with the appropriate set of creation operators.
Jim Branson 2013-04-22