Expansion of a State in Plane Waves

To show how the negative energy states play a role in Zitterbewegung, it is convenient to go back to the Schrödinger representation and expand an arbitrary state in terms of plane waves. As with non-relativistic quantum mechanics, the (free particle) definite momentum states form a complete set and we can expand any state in terms of them.

$$\bgroup\color{black} \psi(\vec{x},t)=\sum\limits_{\vec{p}}\su... ... u^{(r)}_{\vec{p}} e^{i(\vec{p}\cdot\vec{x}-Et)/\hbar} \egroup$$

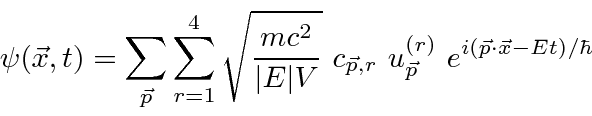
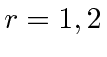The $r=1,2$ terms are positive energy plane waves and the 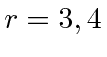$r=3,4$ states are ``negative energy''. The differing signs of the energy in the time behavior will give rise to rapid oscillations.

The plane waves can be purely either positive or ``negative energy'', however, localized states have uncertainty in the momentum and tend to have both positive and ``negative energy'' components. As the momentum components become relativistic, the ``negative energy'' amplitude becomes appreciable.

$$\bgroup\color{black} {c_{3,4}\over c_{1,2}}\approx {pc\over E+mc^2} \egroup$$

Even the Hydrogen bound states have small ``negative energy'' components.

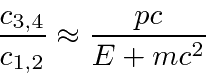
The cross terms between positive and ``negative energy'' will give rise to very rapid oscillation of the expected values of both velocity and position. The amplitude of the oscillations is small for non-relativistic electrons but grows with momentum (or with localization).