Next: Expansion of a State Up: Phenomena of Dirac States Previous: Phenomena of Dirac States Contents
We will work for a while in the Heisenberg representation in which the operators depend on time and we can see some of the general behavior of electrons. If we work in a state of definite energy, the time dependence of the operators is very simple, just the usual exponentials.
The operator for velocity in the x direction can be computed from the commutator with the Hamiltonian.
![\begin{eqnarray*}
\dot{x}={i\over\hbar}[H,x]={i\over\hbar}ic[\gamma_4\gamma_jp_j,x]=ic\gamma_4\gamma_1 \\
v_j=ic\gamma_4\gamma_j \\
\end{eqnarray*}](img4372.png)
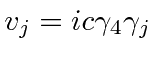 .
.
Its not hard to compute that the velocity eigenvalues (any component) are
![]() .
.
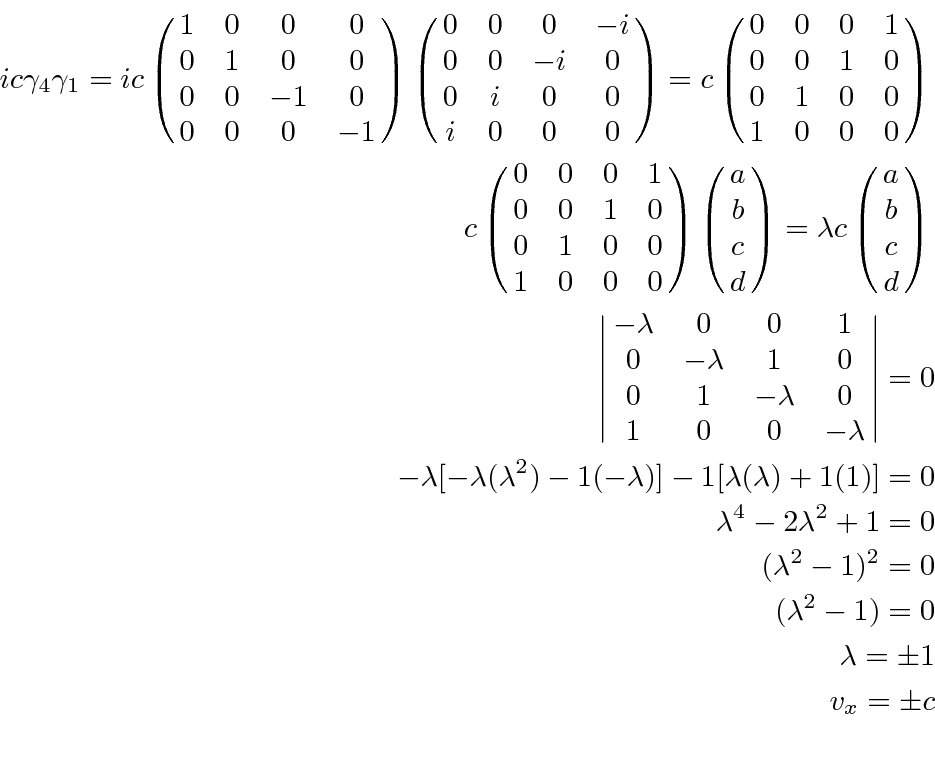
The states of definite momentum are not eigenstates of velocity for a massive electron. The velocity eigenstates mix positive and ``negative energy'' states equally.
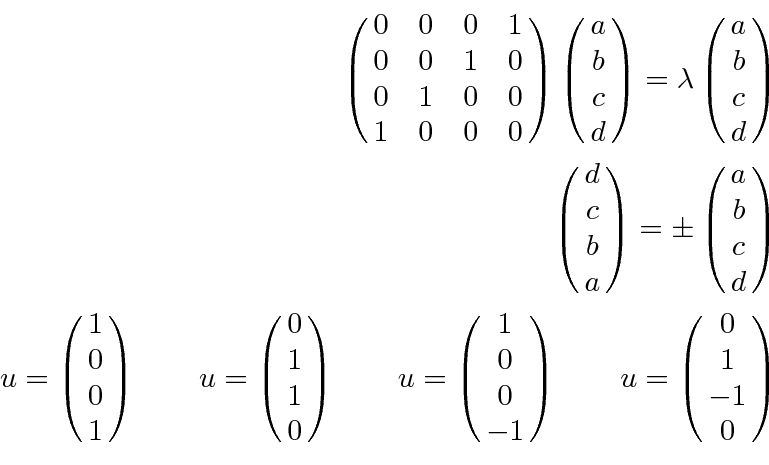
Thus, while momentum is a constant of the motion for a free electron and behaves as it did in NR Quantum Mechanics, velocity behaves very strangely in the Dirac theory, even for a free electron. Some further study of this effect is in order to see if there are physical consequences and what is different about the Dirac theory in this regard.
We may get the differential equation for the velocity of a free electron by computing the derivative of velocity.
We attempt to write the derivative in terms of the constants of the motion
![]() and
and
![]() .
.
![\begin{eqnarray*}
\dot{v}_j&=&{i\over\hbar}[H,v_j]={i\over\hbar}(-2Hv_j+\{H,v_j\...
...{i\over\hbar}(-2Hv_j+2v_j^2p_j)={i\over\hbar}(-2Hv_j+2c^2p_j)\\
\end{eqnarray*}](img4376.png)
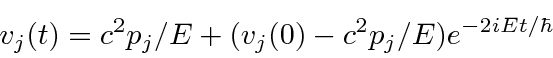
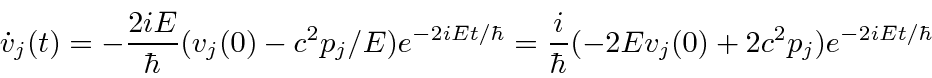
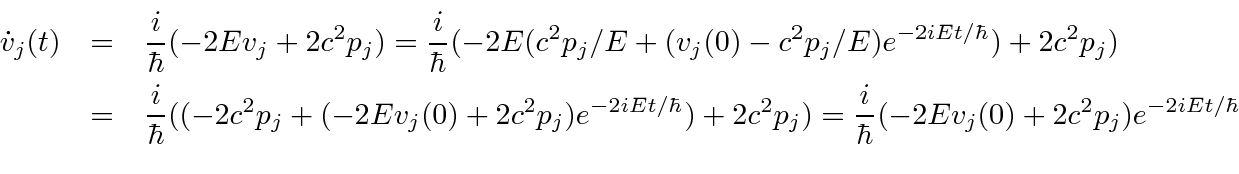
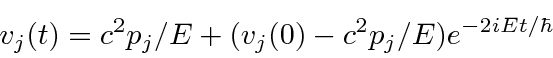
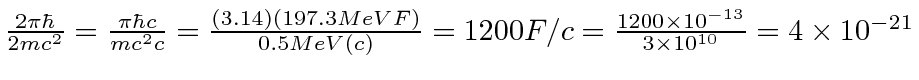 seconds.
This very rapid oscillation is known as Zitterbewegung.
Obviously, we would see the same kind of oscillation in the position if we integrate the above solution for the velocity.
This very rapid motion of the electron means we cannot localize the electron extremely well and gives rise to the Darwin term.
This operator analysis is not sufficient to fully understand the effect of Zitterbewegung but it illustrates the behavior.
seconds.
This very rapid oscillation is known as Zitterbewegung.
Obviously, we would see the same kind of oscillation in the position if we integrate the above solution for the velocity.
This very rapid motion of the electron means we cannot localize the electron extremely well and gives rise to the Darwin term.
This operator analysis is not sufficient to fully understand the effect of Zitterbewegung but it illustrates the behavior.
Jim Branson 2013-04-22