Vibrational States

We have seen that the energy of a molecule has a minimum for some particular separation between atoms. This looks just like a harmonic oscillator potential for small variations from the minimum. The molecule can ``vibrate'' in this potential giving rise to a harmonic oscillator energy spectrum.

We can estimate the energy of the vibrational levels. If 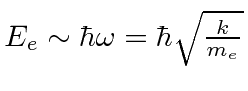$E_e\sim\hbar\omega=\hbar\sqrt{k\over{m_e}}$, then crudely the proton has the same spring constant $\sqrt{k}\approx {E_e\sqrt{m_e}\over\hbar}$.

$$\bgroup\color{black}E_{vib}\sim\hbar \sqrt{k\over M}=\sqrt{m\over M}E_e\sim{1\over {10}}\mbox{ eV}\egroup$$

Recalling that room temperature is about ${1\over 40}$ eV, this is approximately thermal energy, infrared. The energy levels are simply

$$\bgroup\color{black}E=(n+{1\over 2})\hbar\omega_{vib}\egroup$$

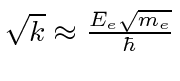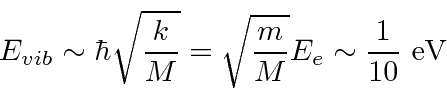
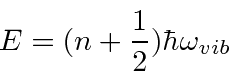
Complex molecules can have many different modes of vibration. Diatomic molecules have just one.

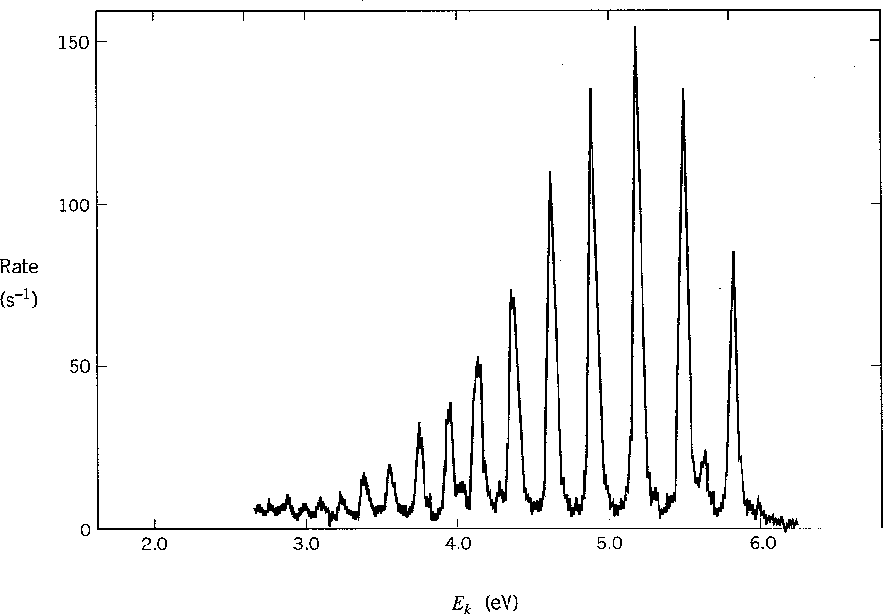
The graph below shows the energy spectrum of electrons knocked out of molecular hydrogen by UV photons (photoelectric effect). The different peaks correspond to the vibrational state of the final H$_2^+$ ion.

Can you calculate the number of vibrational modes for a molecule compose of 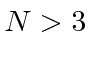$N>3$ atoms.