Next: Examples Up: Molecular Physics Previous: Vibrational States Contents
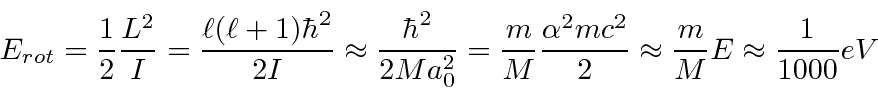
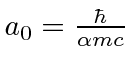 .
These states are strongly excited at room temperature.
.
These states are strongly excited at room temperature.
Let's look at the energy changes between states as we might get in a radiative transition with
![]() ..
..
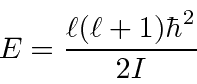
![\begin{displaymath}\bgroup\color{black}\Delta E= {\hbar^2\over{2I}}\left[ \ell(\...
...right]
= {\hbar^2\over{2I}}(2\ell)={\hbar^2\ell\over I} \egroup\end{displaymath}](img3498.png)
With identical nuclei,
![]() is required to be even for (nuclear) spin singlet
and odd for triplet.
This means steps will be larger.
is required to be even for (nuclear) spin singlet
and odd for triplet.
This means steps will be larger.
A complex molecule will have three principle axes, and hence, three moments of inertia to use in our quantized formula.
Counting degrees of freedom, which should be equal to the number of quantum numbers needed to describe the state, we have 3 coordinates to give the position of the center of mass, 3 for the rotational state, and 3N-6 for vibrational. This formula should be modified if the molecule is too simple to have three principle axes.
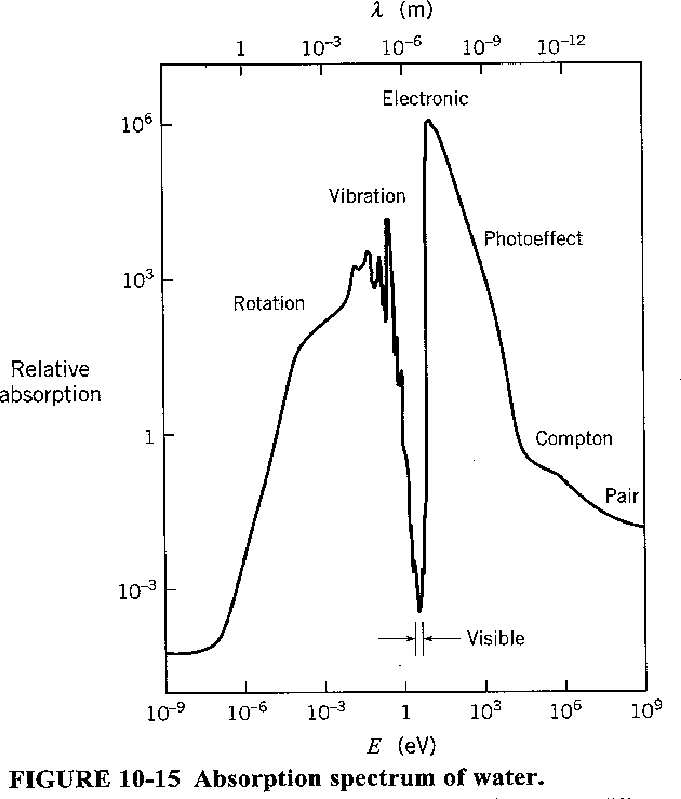
The graph below shows the absorption coefficient of water for light of various energies. For low energies, rotational and vibrational states cause the absorption of light. At higher energies, electronic excitation and photoelectric effect take over. It is only in the region around the visible spectrum that water transmits light well. Can you think of a reason for that?
Jim Branson 2013-04-22