Molecular Orbitals

Even with additional parameters, parity symmetry in diatomic molecules implies we will have symmetric and antisymmetric wavefunctions for single electrons. The symmetric or bonding state has a larger probability to be between the two nuclei, sees more positive charge, and is therefore lower energy. As in our simple model of a molecule, the kinetic energy can be lowered by sharing an electron.

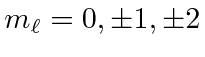There is an axis of symmetry for diatomic molecules. This means $L_z$ commutes with $H$ and $m_\ell$ is a good quantum number. The different $m_\ell$ states, we have seen, have quite different shapes therefore bond differently. Imagine that a valence electron is in a $d$ state. The $m_\ell=0,\pm 1,\pm 2$ are called molecular orbitals 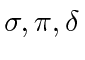$\sigma,\pi,\delta$ respectively. Each has a bonding and an antibonding state.

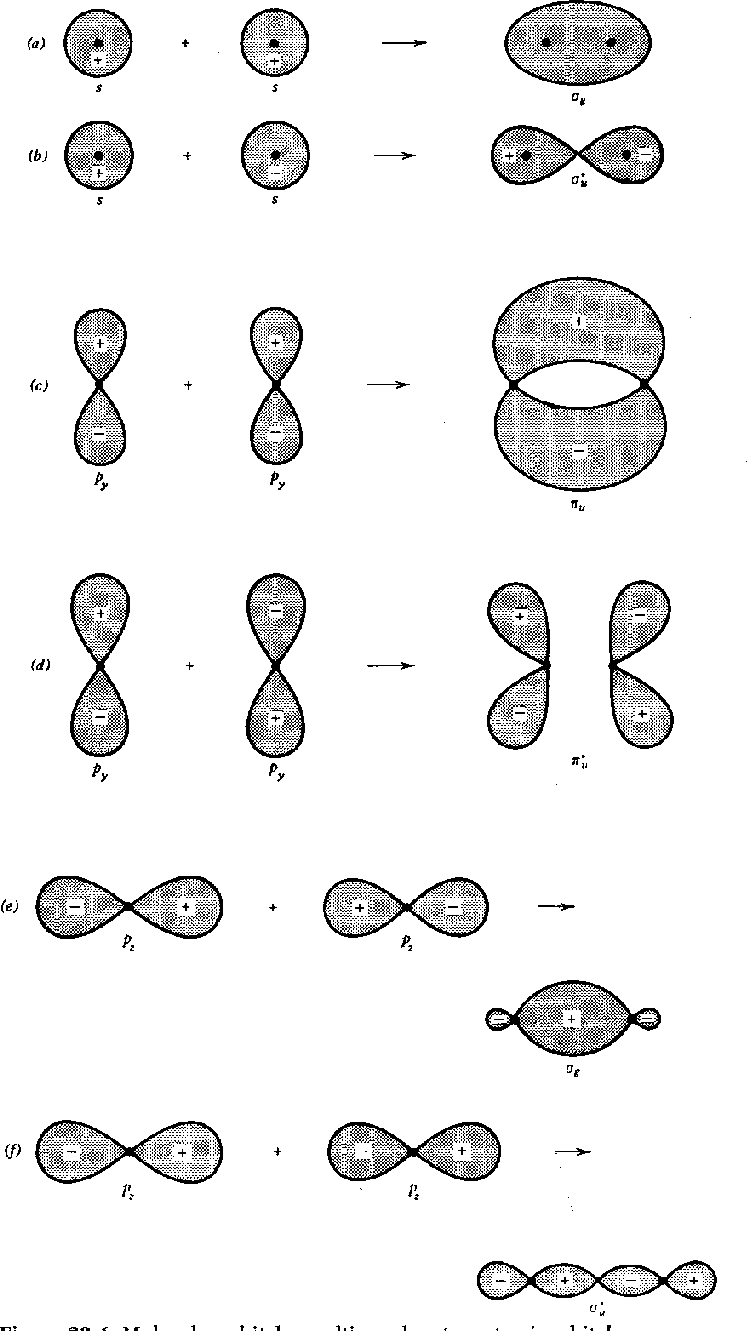
Pictures of molecular orbitals are shown for $s$ and $p$ states in the following figure. Both bonding and antibonding orbitals are shown first as atomic states then as molecular. The antibonding states are denoted by a *.