Next: Variational Helium Ground State Up: The Helium Atom Previous: The First Excited State(s) Contents
Because the ground state has the lowest possible energy,
we can vary a test wavefunction, minimizing the energy,
to get a good estimate of the ground state energy.
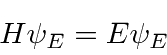
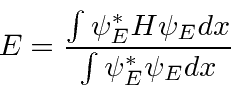
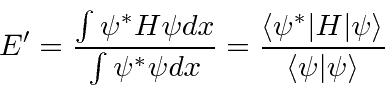
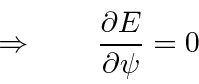
To do this, we will add a variable amount of an arbitrary function
![]() to the energy eigenstate.
to the energy eigenstate.
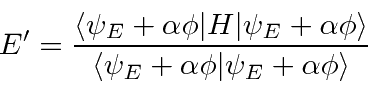
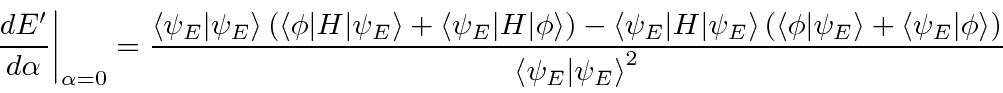
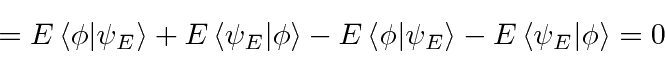
That is,
![]() is stationary (2nd order changes only) with respect to variation in
is stationary (2nd order changes only) with respect to variation in
![]() .
Conversely, it can be shown that
.
Conversely, it can be shown that
![]() is only stationary for eigenfunctions
is only stationary for eigenfunctions
![]() .
We can use the variational principle to approximately find
.
We can use the variational principle to approximately find
![]() and to find an upper bound on
and to find an upper bound on
![]() .
.
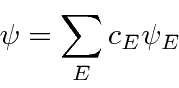
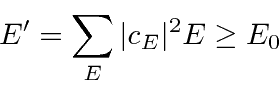
* Example:
Energy of 1D Harmonic Oscillator using a polynomial trail wave function.*
* Example:
1D H.O. using Gaussian.*
Jim Branson 2013-04-22