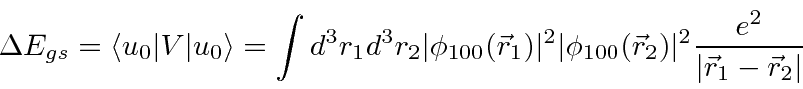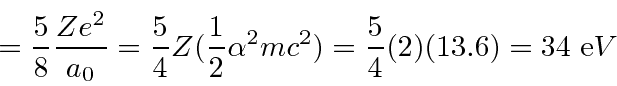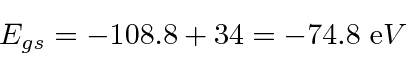The Helium Ground State

Calculating the first order correction to the ground state is simple in principle.

$$\bgroup\color{black} \Delta E_{gs} = \left<u_0 \vert V \vert ... ...rt^2 { e^2\over{ \vert\vec{r}_1 - \vec{r}_2\vert }} } \egroup$$

$$\bgroup\color{black} = {5\over 8}{Ze^2\over {a_0}} = {5\over ... ...alpha^2mc^2) = {5\over 4} (2) (13.6) = 34 {\mathrm eV}\egroup$$

The calculation of the energy shift in first order involves an integral over the coordinates of both electrons.

So the ground state energy to first order is

$$\bgroup\color{black}E_{gs}=-108.8+34=-74.8 {\mathrm eV}\egroup$$

compared to -78.975 eV from experiment. A 10% error is not bad considering the size of the perturbation. First order perturbation theory neglects the change in the electron's wavefunction due to screening of the nuclear charge by the other electron. Higher order perturbation theory would correct this, however, it is hard work doing that infinite sum. We will find a better way to improve the calculation a bit.