Next: Time Dependent Perturbation Theory Up: Course Summary Previous: Atomic Physics Contents
We can study
simple molecules
to understand the physical phenomena of molecules in general.
The simplest molecule we can work with is the
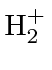 ion.
It has two nuclei (A and B) sharing one electron (1).
ion.
It has two nuclei (A and B) sharing one electron (1).
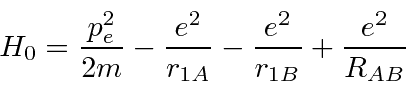
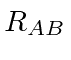 is the distance between the two nuclei.
We calculate the ground state energy using the Hydrogen states as a basis.
is the distance between the two nuclei.
We calculate the ground state energy using the Hydrogen states as a basis.
The lowest energy wavefunction can be thought of as a (anti)symmetric linear combination of an
electron in the ground state near nucleus A and the ground state near nucleus B
![\begin{displaymath}\bgroup\color{black}\psi_\pm\left(\vec{r},\vec{R}\right)=C_\pm(R)\left[\psi_A\pm\psi_B\right]\egroup\end{displaymath}](img370.png)
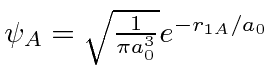 is g.s. around nucleus A.
is g.s. around nucleus A.
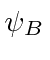 are not orthogonal; there is overlap.
The symmetric (bonding) state has a large probability for the electron to be found between nuclei.
The antisymmetric (antibonding) state has a small probability there, and hence,
a much larger energy.
Remember, this symmetry is that of the wavefunction of one electron around the two nuclei.
are not orthogonal; there is overlap.
The symmetric (bonding) state has a large probability for the electron to be found between nuclei.
The antisymmetric (antibonding) state has a small probability there, and hence,
a much larger energy.
Remember, this symmetry is that of the wavefunction of one electron around the two nuclei.
The ![]() molecule is also simple and its energy can be computed with the help of the previous calculation.
The space symmetric state will be the ground state.
molecule is also simple and its energy can be computed with the help of the previous calculation.
The space symmetric state will be the ground state.
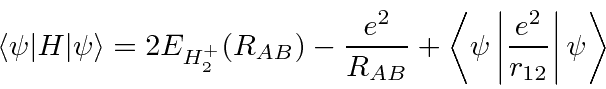
Molecules can rotate like classical rigid bodies subject to the constraint that angular
momentum is quantized in units of
![]() .
.
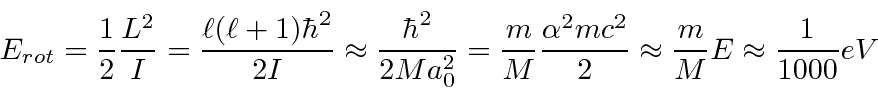
Jim Branson 2013-04-22