Next: Molecules Up: Course Summary Previous: The Helium Atom Contents
The Hamiltonian for an
atom with Z electrons and protons
has many terms representing the repulsion between each pair of electrons.
![\begin{displaymath}\bgroup\color{black}\left[ \sum\limits^Z_{i=1} \left({p^2_i\o...
...\vert\vec{r_i}-\vec{r_j}\right\vert}} \right]\psi=E\psi.\egroup\end{displaymath}](img361.png)
The physics of closed shells and angular momentum enable us to
make sense of even the most complex atoms.
When we have enough electrons to fill a shell, say the 1s or 2p, The resulting
electron distribution is spherically symmetric because
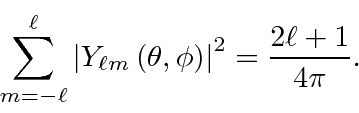
The closed shell screens the nuclear charge.
Because of the screening, the potential no longer has a pure
![]() behavior.
Electrons which are far away from the nucleus see less of the nuclear charge and shift up
in energy.
We see that the atomic shells fill up in the order 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p.
The effect of screening increasing the energy of higher
behavior.
Electrons which are far away from the nucleus see less of the nuclear charge and shift up
in energy.
We see that the atomic shells fill up in the order 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p.
The effect of screening increasing the energy of higher
![]() states is clear.
Its no wonder that the periodic table is not completely periodic.
states is clear.
Its no wonder that the periodic table is not completely periodic.
A set of guidelines, known as Hund's rules, help us determine the quantum numbers for the
ground states of atoms.
The hydrogenic shells fill up giving well defined
 states for the closed shells.
As we add valence electrons we follow Hund's rules to determine the ground state.
We get a great simplification by treating nearly closed shells as a closed shell plus
positively charged, spin
states for the closed shells.
As we add valence electrons we follow Hund's rules to determine the ground state.
We get a great simplification by treating nearly closed shells as a closed shell plus
positively charged, spin
![]() holes.
For example, if an atom is two electrons short of a closed shell,
we treat it as a closed shell plus two positive holes.)
holes.
For example, if an atom is two electrons short of a closed shell,
we treat it as a closed shell plus two positive holes.)
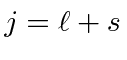 otherwise pick the lowest
otherwise pick the lowest 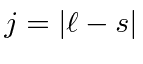 .
.
Jim Branson 2013-04-22