The Helium Atom

The Hamiltonian for Helium has the same terms as Hydrogen but has a large perturbation due to the repulsion between the two electrons.

$$\bgroup\color{black} H = {p^2_1\over{2m}} + {p^2_2\over{2m}} ... ...{r_2}} + {e^2\over{ \vert\vec{r}_1 - \vec{r}_2\vert }} \egroup$$

Note that the perturbation due to the repulsion between the two electrons is about the same size as the the rest of the Hamiltonian so first order perturbation theory is unlikely to be accurate.

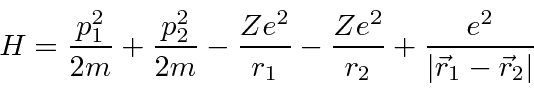
The Helium ground state has two electrons in the 1s level. Since the spatial state is symmetric, the spin part of the state must be antisymmetric so $s=0$ (as it always is for closed shells). For our zeroth order energy eigenstates, we will use product states of Hydrogen wavefunctions

$$\bgroup\color{black} u(\vec{r}_1,\vec{r}_2) = \phi_{n_1 \ell_1 m_1}(\vec{r}_1) \phi_{n_2 \ell_2 m_2}(\vec{r}_2) \egroup$$

and ignore the perturbation. The energy for two electrons in the (1s) state for $Z=2$ is then $4\alpha^2mc^2=108.8$ eV.

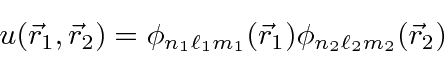
We can estimate the ground state energy in first order perturbation theory, using the electron repulsion term as a (very large) perturbation. This is not very accurate.

We can improve the estimate of the ground state energy using the variational principle. The main problem with our estimate from perturbation theory is that we are not accounting for changes in the wave function of the electrons due to screening. We can do this in some reasonable approximation by reducing the charge of the nucleus in the wavefunction (not in the Hamiltonian). With the parameter $Z^*$, we get a better estimate of the energy.

Calculation	Energy	$Z_{wfn}$
$0^{th}$ Order	-108.8	2
$1^{st}$ Order perturbation theory	-74.8	2
$1^{st}$ Order Variational	-77.38	${27\over 16}$
Actual	-78.975

Note that the variational calculation still uses first order perturbation theory. It just adds a variable parameter to the wavefunction which we use to minimize the energy. This only works for the ground state and for other special states.

There is only one allowed 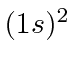$(1s)^2$ state and it is the ground state. For excited states, the spatial states are (usually) different so they can be either symmetric or antisymmetric (under interchange of the two electrons). It turns out that the antisymmetric state has the electrons further apart so the repulsion is smaller and the energy is lower. If the spatial state is antisymmetric, then the spin state is symmetric, s=1. So the triplet states are generally significantly lower in energy than the corresponding spin singlet states. This appears to be a strong spin dependent interaction but is actually just the effect of the repulsion between the electrons having a big effect depending on the symmetry of the spatial state and hence on the symmetry of the spin state.

The first exited state has the hydrogenic state content of (1s)(2s) and has s=1. We calculated the energy of this state.

We'll learn later that electromagnetic transitions which change spin are strongly suppressedcausing the spin triplet (orthohelium) and the spin singlet states (parahelium) to have nearly separate decay chains.