Next: The Helium Atom Up: Course Summary Previous: The Fine Structure of Contents
The interaction between the spin of the nucleus and the angular momentum of the electron
causes a further
(hyperfine) splitting
of atomic states.
It is called hyperfine because it is also order
![]() like the fine structure corrections, but it is smaller
by a factor of about
like the fine structure corrections, but it is smaller
by a factor of about
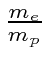 because of the mass dependence of the spin magnetic moment for particles.
because of the mass dependence of the spin magnetic moment for particles.
The magnetic moment of the nucleus is
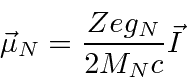
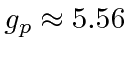 .
.
We computed the hyperfine contribution to the Hamiltonian for
![]() states.
states.
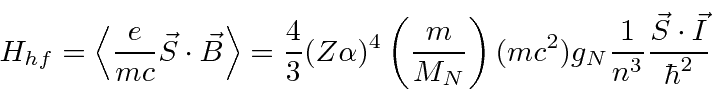
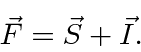
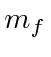 that the hyperfine perturbation
will be diagonal.
In essence, we are doing degenerate state perturbation theory.
We could diagonalize the 4 by 4 matrix for the perturbation to solve the problem or
we can use what we know to pick the right states to start with.
Again like the spin orbit interaction, the total angular momentum states will be
the right states because we can write the perturbation in terms of
quantum numbers of those states.
that the hyperfine perturbation
will be diagonal.
In essence, we are doing degenerate state perturbation theory.
We could diagonalize the 4 by 4 matrix for the perturbation to solve the problem or
we can use what we know to pick the right states to start with.
Again like the spin orbit interaction, the total angular momentum states will be
the right states because we can write the perturbation in terms of
quantum numbers of those states.
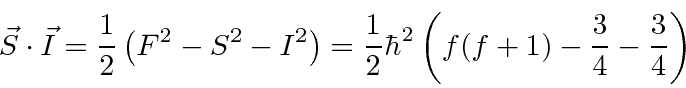
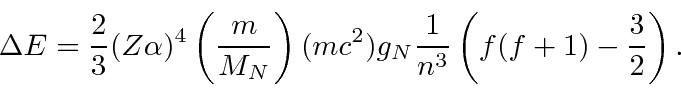
For the hydrogen ground state we are just adding two spin
![]() particles so the
possible values are
particles so the
possible values are
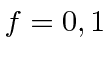 .
The transition between the two states gives rise to EM waves with
.
The transition between the two states gives rise to EM waves with
![]() cm.
cm.
We will work out the effect of an external B field on the Hydrogen hyperfine statesboth in the strong field and in the weak field approximation. We also work the problem without a field strength approximation. The always applicable intermediate field strength result is that the four states have energies which depend on the strength of the B field. Two of the energy eigenstates mix in a way that also depends on B. The four energies are
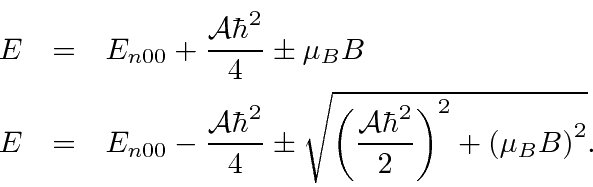
Jim Branson 2013-04-22