Time Dependent Perturbation Theory

We have used time independent perturbation theory to find the energy shifts of states and to find the change in energy eigenstates in the presence of a small perturbation. We now consider the case of a perturbation ${\cal V}$ that is time dependent. Such a perturbation can cause transitions between energy eigenstates. We will calculate the rate of those transitions.

We derive an equation for the rate of change of the amplitude to be in the $n^{th}$ energy eigenstate.

$$\begin{eqnarray*} i\hbar{\partial c_n(t)\over\partial t}&=&\sum\limits_k {\cal V}_{nk}(t) c_k(t)e^{i(E_n-E_k)t/\hbar} \\ \end{eqnarray*}$$

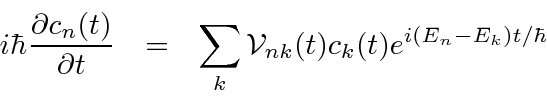
Assuming that at $t=0$ the quantum system starts out in some initial state $\phi_i$, we derive the amplitude to be in a final state $\phi_n$.

$$\bgroup\color{black} c_n(t)={1\over i\hbar}\int\limits_0^te^{i\omega_{ni}t'}{\cal V}_{ni}(t')dt' \egroup$$

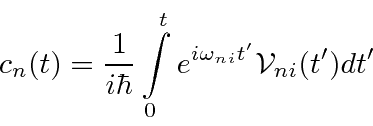
An important case of a time dependent potential is a pure sinusoidal oscillating (harmonic) perturbation. We can make up any time dependence from a linear combination of sine and cosine waves. With some calculation, we derive the transition rate in a harmonic potential of frequency $\omega$.

$$\bgroup\color{black} \Gamma_{i\rightarrow n}\equiv {dP_n\over... ...= {2\pi V_{ni}^2\over \hbar}\delta(E_n-E_i+\hbar\omega) \egroup$$

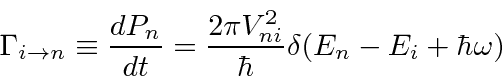
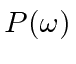This contains a delta function of energy conservation. The delta function may seem strange. The transition rate would be zero if energy is not conserved and infinite if energy is exactly conserved. We can make sense of this if there is a distribution function of $P(\omega)$ of the perturbing potential or if there is a continuum of final states that we need to integrate over. In either case, the delta function helps us do the integral simply.