- A particle is in the state
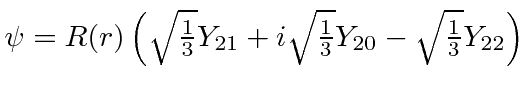 .
Find the expected values of
.
Find the expected values of 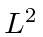 ,
, 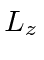 ,
, 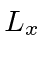 , and
, and 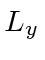 .
.
- A particle is in the state
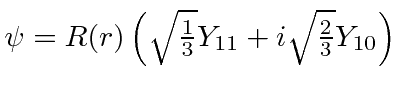 .
If a measurement of the
.
If a measurement of the 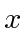 component of angular momentum is made, what are the possilbe outcomes
and what are the probabilities of each?
component of angular momentum is made, what are the possilbe outcomes
and what are the probabilities of each?
- Calculate the matrix elements
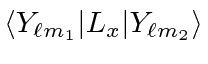 and
and
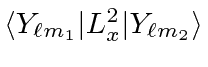
- The Hamiltonian for a rotor with axial symmetry is
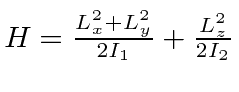 where the
where the 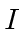 are constant moments of inertia.
Determine and plot the eigenvalues of
are constant moments of inertia.
Determine and plot the eigenvalues of 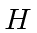 for dumbbell-like case that
for dumbbell-like case that 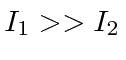 .
.
- Prove that
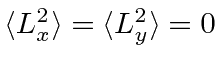 is only possible for
is only possible for 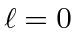 .
.
- Write the spherical harmonics for
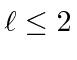 in terms of the Cartesian coordinates
in terms of the Cartesian coordinates 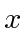 ,
, 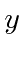 , and
, and 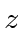 .
.
- A particle in a spherically symmetric potential has the wave-function
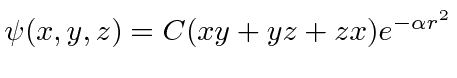 .
A measurement of
.
A measurement of 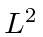 is made.
What are the possible results and the probabilities of each?
If the measurement of
is made.
What are the possible results and the probabilities of each?
If the measurement of 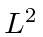 yields
yields 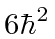 , what are the possible measured values of
, what are the possible measured values of 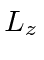 and what are the corresponding probabilities?
and what are the corresponding probabilities?
- The deuteron, a bound state of a proton and neutron with
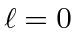 , has a binding energy of -2.18 MeV.
Assume that the potential is a spherical well with potential of
, has a binding energy of -2.18 MeV.
Assume that the potential is a spherical well with potential of 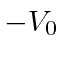 for
for 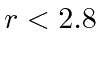 Fermis and zero potential outside.
Find the approximate value of
Fermis and zero potential outside.
Find the approximate value of 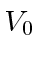 using numerical techniques.
using numerical techniques.
Jim Branson
2013-04-22
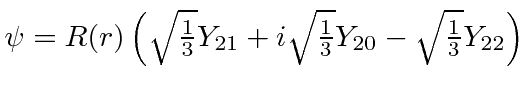 .
Find the expected values of
.
Find the expected values of 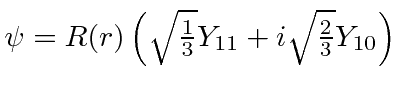 .
If a measurement of the
.
If a measurement of the 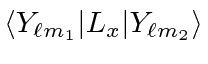 and
and
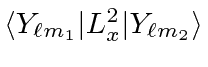
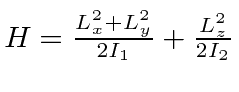 where the
where the 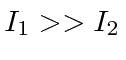 .
.
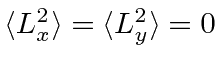 is only possible for
is only possible for 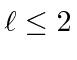 in terms of the Cartesian coordinates
in terms of the Cartesian coordinates 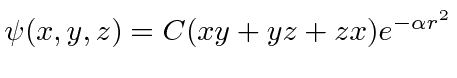 .
A measurement of
.
A measurement of 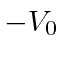 for
for 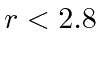 Fermis and zero potential outside.
Find the approximate value of
Fermis and zero potential outside.
Find the approximate value of