- The energy spectrum of hydrogen can be written in terms of
the principal quantum number
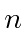 to be
to be
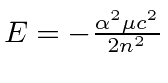 .
What are the energies (in eV) of the photons from the
.
What are the energies (in eV) of the photons from the
 transition
in hydrogen and deuterium?
What is the difference in photon energy between the two isotopes of hydrogen?
transition
in hydrogen and deuterium?
What is the difference in photon energy between the two isotopes of hydrogen?
- Prove that the operator that exchanges two identical particles is Hermitian.
- Two identical, non-interacting spin
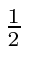 particles are in a box.
Write down the full lowest energy wave function for both particles with spin up
and for one with spin up and the other spin down.
Be sure your answer has the correct symmetry under the interchange of identical particles.
particles are in a box.
Write down the full lowest energy wave function for both particles with spin up
and for one with spin up and the other spin down.
Be sure your answer has the correct symmetry under the interchange of identical particles.
- At
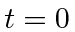 a particle is in the one dimensional Harmonic Oscillator state
a particle is in the one dimensional Harmonic Oscillator state
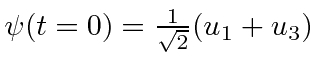 .
Compute the expected value of
.
Compute the expected value of 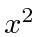 as a function of time.
as a function of time.
- Calculate the Fermi energy of a gas of massless fermions with
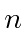 particles per unit volume.
particles per unit volume.
- The number density of conduction electrons in copper is
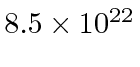 per cubic centimeter.
What is the Fermi energy in electron volts?
per cubic centimeter.
What is the Fermi energy in electron volts?
- The volume of a nucleus is approximately
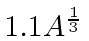 Fermis,
where
Fermis,
where 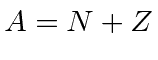 ,
, 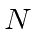 is the number of neutrons, and
is the number of neutrons, and 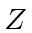 is the number of protons.
A Lead nucleus consists of 82 protons and 126 neutrons.
Estimate the Fermi energy of the protons and neutrons separately.
is the number of protons.
A Lead nucleus consists of 82 protons and 126 neutrons.
Estimate the Fermi energy of the protons and neutrons separately.
- The momentum operator conjugate to any cooridinate
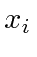 is
is
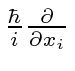 .
Calculate the commutators of the center of mass coordinates and momenta
.
Calculate the commutators of the center of mass coordinates and momenta ![$[P_i,R_j]$](img2565.png) and of the internal coordinates and momenta
and of the internal coordinates and momenta ![$[p_i,r_j]$](img2566.png) .
Calculate the commutators
.
Calculate the commutators ![$[P_i,r_j]$](img2567.png) and
and ![$[p_i,R_j]$](img2568.png) .
.
Jim Branson
2013-04-22
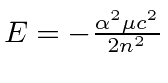 .
What are the energies (in eV) of the photons from the
.
What are the energies (in eV) of the photons from the
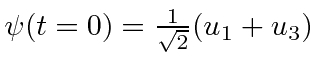 .
Compute the expected value of
.
Compute the expected value of 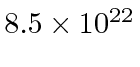 per cubic centimeter.
What is the Fermi energy in electron volts?
per cubic centimeter.
What is the Fermi energy in electron volts?
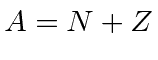 ,
, 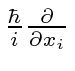 .
Calculate the commutators of the center of mass coordinates and momenta
.
Calculate the commutators of the center of mass coordinates and momenta ![$[P_i,R_j]$](img2565.png) and of the internal coordinates and momenta
and of the internal coordinates and momenta ![$[p_i,r_j]$](img2566.png) .
Calculate the commutators
.
Calculate the commutators ![$[P_i,r_j]$](img2567.png) and
and ![$[p_i,R_j]$](img2568.png) .
.