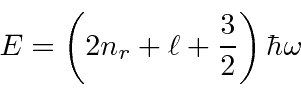Solution of the 3D HO Problem in Spherical Coordinates

As and example of another problem with spherical symmetry, we solve the 3D symmetric harmonic oscillator problem. We have already solved this problem in Cartesian coordinates. Now we use spherical coordinates and angular momentum eigenfunctions.

The eigen-energies are

$$\bgroup\color{black} E=\left(2n_r+\ell+{3\over 2}\right)\hbar\omega \egroup$$

where $n_r$ is the number of nodes in the radial wave function and $\ell$ is the total angular momentum quantum number. This gives exactly the same set of eigen-energies as we got in the Cartesian solution but the eigenstates are now states of definite total angular momentum and z component of angular momentum.