Next: Sample Test Problems Up: Examples Previous: Compton Scattering * Contents
To solve this, we need to compute the potential at the center of the charge distribution relative to the potential at infinity (which we will say is zero). This tells us directly the kinetic energy in eV needed to plow right through the charge distribution.
The potential at the surface of the nucleus is
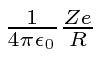 where Z is the number of protons in the atom and R is the nuclear radius.
That's the easy part. Now we need to integrate our way into the center.
where Z is the number of protons in the atom and R is the nuclear radius.
That's the easy part. Now we need to integrate our way into the center.
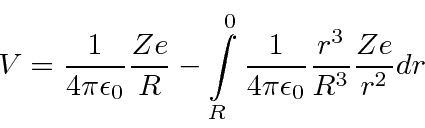
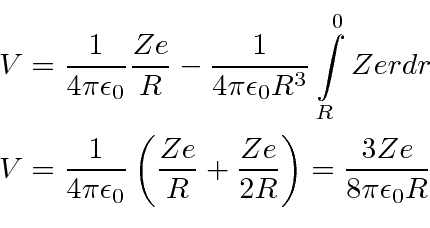
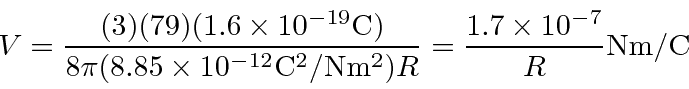
The is then the kinetic energy in eV needed for a particle of charge
![]() to plow right through the
center of a spherical charge distribution.
The
to plow right through the
center of a spherical charge distribution.
The
![]() particle actually has charge
particle actually has charge
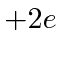 so we need to multiply by 2.
For a nuclear radius of 5 Åor
so we need to multiply by 2.
For a nuclear radius of 5 Åor
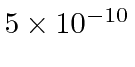 meters, we need about 680 eV to plow through the nucleus.
For the actual nuclear radius of about 5 Fermis or
meters, we need about 680 eV to plow through the nucleus.
For the actual nuclear radius of about 5 Fermis or
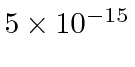 meters, we need 68 MeV to plow through.
meters, we need 68 MeV to plow through.
Lets compare the above SI units numbers to my suggested method of using the fine structure constant...
Putting in the alpha charge of
![]() .
.
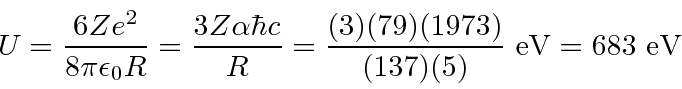
Jim Branson 2013-04-22