Next: Rutherford's Nuclear Size * Up: Examples Previous: Black Body Radiation from Contents
Compton scattered high energy photons from (essentially) free electrons in 1923.
He measured the wavelength of the scattered photons as a function of the scattering angle.
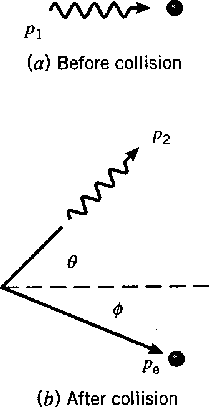
The figure below shows both the initial state (a) and the final state, with the photon
scattered by an angle
![]() and the electron recoiling at an angle
and the electron recoiling at an angle
![]() .
The photons were from nuclear decay and so they were of high enough energy that it
didn't matter that the electrons were actually bound in atoms.
We wish to derive the formula for the wavelength of the scattered photon as a function of angle.
.
The photons were from nuclear decay and so they were of high enough energy that it
didn't matter that the electrons were actually bound in atoms.
We wish to derive the formula for the wavelength of the scattered photon as a function of angle.
We solve the problem using only conservation of energy and momentum.
Lets work in units in which
![]() for now. We'll put the
for now. We'll put the
![]() back in at the end.
Assume the photon is initially moving in the
back in at the end.
Assume the photon is initially moving in the
![]() direction with energy E
and that it scatters in the
direction with energy E
and that it scatters in the
![]() plane so that
plane so that
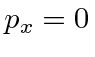 .
Conservation of momentum gives
.
Conservation of momentum gives
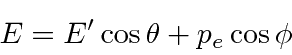
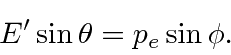
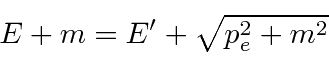
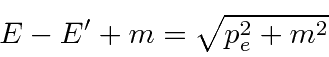
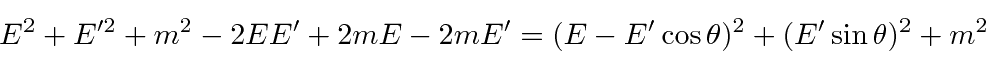
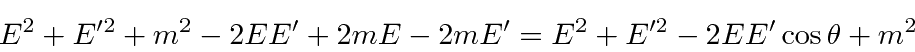
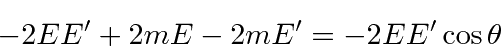
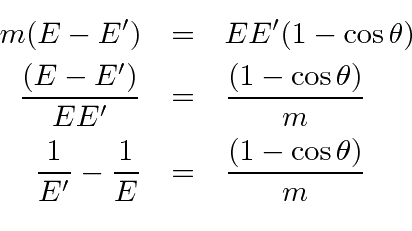
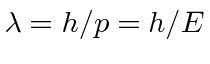 in our fine units,
in our fine units,
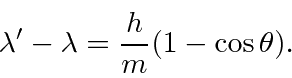
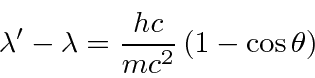
These calculations can be fairly frustrating if you don't decide which variables you want to keep and which
you need to eliminate from your equations.
In this case we eliminated
![]() by using the energy equation and computing
by using the energy equation and computing
![]() .
.
Jim Branson 2013-04-22