Next: Two Examples of Localized Up: Wave Packets Previous: Wave Packets Contents
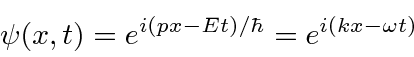
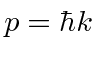 and the angular frequency
and the angular frequency
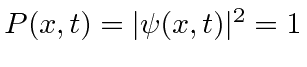 everywhere.
everywhere.
We would like a state which is localized and normalized to one particle.
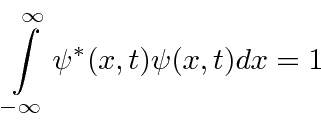
To make a wave packet which is localized in space,
we must add components of different wave number.
Recall that we can use a
Fourier Series
to compose any function
 when we limit the range to
when we limit the range to
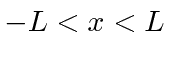 .
We do not want to limit our states in
.
We do not want to limit our states in
![]() , so we will take the limit that
, so we will take the limit that
![]() .
In that limit, every wave number is allowed so the sum turns into an integral.
The result is the very closely related
Fourier Transform
.
In that limit, every wave number is allowed so the sum turns into an integral.
The result is the very closely related
Fourier Transform
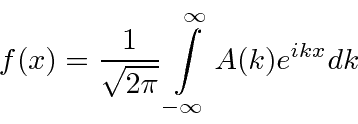
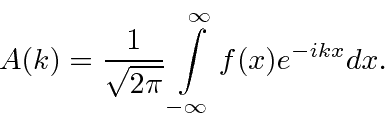
The normalizations of
 and
and
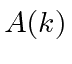 are the same
(with this symmetric form)
and both can represent probability amplitudes.
are the same
(with this symmetric form)
and both can represent probability amplitudes.
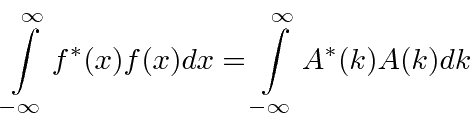
We understand
 as a wave packet made up of definite momentum terms
as a wave packet made up of definite momentum terms
![]() .
The coefficient of each term is
.
The coefficient of each term is
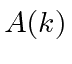 .
The probability for a particle to be found in a region
.
The probability for a particle to be found in a region
![]() around some value of
around some value of
![]() is
is
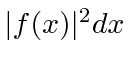 .
The probability for a particle to have wave number in region
.
The probability for a particle to have wave number in region
![]() around some value of
around some value of
![]() is
is
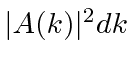 .
(Remember that
.
(Remember that
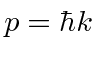 so the momentum distribution is very closely related.
We work with
so the momentum distribution is very closely related.
We work with
![]() for a while for economy of notation.)
for a while for economy of notation.)
Jim Branson 2013-04-22